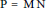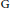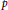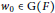Let $\text{P}\,\text{=}\,\text{M}\,\text{N}$ be a Levi decomposition of a maximal parabolic subgroup of a connected reductive group $\text{G}$ over a $p$-adic field $F$. Assume that there exists ${{w}_{0}}\,\in \,G\left( F \right)$ that normalizes 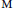$\text{M}$ and conjugates $\text{p}$ to an opposite parabolic subgroup. When 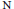$\text{N}$ has a Zariski dense 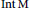$\text{Int}\,\text{M}$-orbit, $\text{F}$. Shahidi and $\text{X}$. Yu described a certain distribution $D$ on 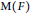$\text{M}\left( F \right)$, such that, for irreducible unitary supercuspidal representations $\pi $ of 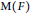$\text{M}\left( F \right)$ with 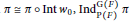$\pi \,\cong \,\pi \,\circ \,\text{Int}\,{{w}_{0}},\,\text{Ind}_{\text{P}\left( F \right)}^{\text{G}\left( F \right)}\,\pi $ is irreducible if and only if 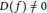$D\left( f \right)\,\ne \,0$ for some pseudocoefficient 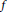$f$ of $\pi $. Since this irreducibility is conjecturally related to $\pi $ arising via transfer from certain twisted endoscopic groups of 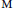$\text{M}$, it is of interest to realize $D$ as endoscopic transfer from a simpler distribution on a twisted endoscopic group 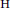$\text{H}$ of 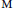$\text{M}$. This has been done in many situations where 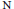$\text{N}$ is abelian. Here we handle the standard examples in cases where 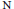$\text{N}$ is nonabelian but admit a Zariski dense 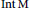$\text{Int}\,\text{M}$-orbit.

Our objective in this sequel to $[18]$ is to develop extensions, to representations of tensor algebras over ${{C}^{*}}$-correspondences, of two fundamental facts about isometries on Hilbert space: The Wold decomposition theorem and Beurling’s theorem, and to apply these to the analysis of the invariant subspace structure of certain subalgebras of Cuntz-Krieger algebras.

This paper is concerned with representations of split orthogonal and quasi-split unitary groups over a nonarchimedean local field which are not generic, but which support a unique model of a different kind, the generalized Bessel model. The properties of the Bessel models under induction are studied, and an analogue of Rodier‘s theorem concerning the induction of Whittaker models is proved for Bessel models which are minimal in a suitable sense. The holomorphicity in the induction parameter of the Bessel functional is established. Local coefficients are defined for each irreducible supercuspidal representation which carries a Bessel functional and also for a certain component of each representation parabolically induced from such a supercuspidal. The local coefficients are related to the Plancherel measures, and their zeroes are shown to be among the poles of the standard intertwining operators.

Let $G$ a compact group of isometries of a closed riemannian manifold $(X,m)$. Sunada proved that if $\Gamma_1$ and $\Gamma_2$ are two finite almost-conjugated subgroups of $G$, then $\Gamma_1\setminus X,m)$ and $\Gamma_2\setminus X,m)$ are isospectral. We prove that if $G$ is finite, there exists an open dense set in the set of $G$-invariant metrics for which the converse of this resukt is true. If $G$ is infinite, the situations is more complicated and we obtain some partial results.