A famous conjecture of Hopf states that 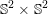 $\mathbb{S}^{2}\times \mathbb{S}^{2}$ does not admit a Riemannian metric with positive sectional curvature. In this article, we prove that no manifold product
$\mathbb{S}^{2}\times \mathbb{S}^{2}$ does not admit a Riemannian metric with positive sectional curvature. In this article, we prove that no manifold product 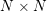 $N\times N$ can carry a metric of positive sectional curvature admitting a certain degree of torus symmetry.
$N\times N$ can carry a metric of positive sectional curvature admitting a certain degree of torus symmetry.