For α ∈ [0, 1] the operator 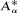 is the operator formally defined on the Hardy space H2 by
is the operator formally defined on the Hardy space H2 by
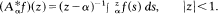
If α = 1, then the usual identification of H2 with l2 takes A1 onto the discrete Cesàro operator. Here we see that {Aα: α ∈ [0, 1]} is not arcwise connected, that Re Aα ≥ 0, that Aα is a Hilbert-Schmidt operator if α ∈[0, 1), and that Aα is neither normaloid nor spectraloid if α ∈(0, 1).