In this paper we establish a Chowla–Selberg formula for abelian CM fields. This is an identity which relates values of a Hilbert modular function at CM points to values of Euler’s gamma function ${\rm\Gamma}$ and an analogous function ${\rm\Gamma}_{2}$ at rational numbers. We combine this identity with work of Colmez to relate the CM values of the Hilbert modular function to Faltings heights of CM abelian varieties. We also give explicit formulas for products of exponentials of Faltings heights, allowing us to study some of their arithmetic properties using the Lang–Rohrlich conjecture.

Abstract. Let 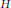$H$ be the Hilbert class field of a 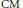$\text{CM}$ number field 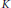$K$ with maximal totally real subfield $F$ of degree $n$ over 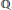$\mathbb{Q}$. We evaluate the second term in the Taylor expansion at 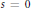$s\,=\,0$ of the Galois-equivariant $L$-function ${{\Theta }_{{{S}_{\infty }}\,}}\left( s \right)$ associated to the unramified abelian characters of 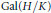$\text{Gal}\left( H/K \right)$. This is an identity in the group ring 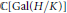$\mathbb{C}\left[ \text{Gal}\left( H/K \right) \right]$ expressing 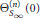$\Theta _{{{S}_{\infty }}}^{(n)}\,\left( 0 \right)$ as essentially a linear combination of logarithms of special values 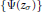$\left\{ \Psi ({{z}_{\sigma }}) \right\}$, where 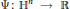$\Psi :\,{{\mathbb{H}}^{n}}\,\to \,\mathbb{R}$ is a Hilbert modular function for a congruence subgroup of 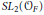$S{{L}_{2}}\left( {{\mathcal{O}}_{F}} \right)$ and $\left\{ {{z}_{\sigma }}\,:\,\sigma \,\in \,\text{Gal}\left( H/K \right) \right\}$ are 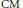$\text{CM}$ points on a universal Hilbert modular variety. We apply this result to express the relative class number 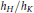${{h}_{H}}/{{h}_{K}}$ as a rational multiple of the determinant of an 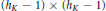$\left( {{h}_{K}}\,-\,1 \right)\,\times \,\left( {{h}_{K}}\,-\,1 \right)$ matrix of logarithms of ratios of special values 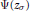$\Psi ({{z}_{\sigma }})$, thus giving rise to candidates for higher analogs of elliptic units. Finally, we obtain a product formula for 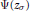$\Psi ({{z}_{\sigma }})$ in terms of exponentials of special values of $L$-functions.