We construct Lipschitz functions such that for all 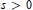 $s>0$ they are
$s>0$ they are 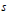 $s$-Hölder, and so proximally, subdifferentiable only on dyadic rationals and nowhere else. As applications we construct Lipschitz functions with prescribed Hölder and approximate subderivatives.
$s$-Hölder, and so proximally, subdifferentiable only on dyadic rationals and nowhere else. As applications we construct Lipschitz functions with prescribed Hölder and approximate subderivatives.