We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We construct a flat model structure on the category ${_{\mathcal {Q},\,R}\mathsf {Mod}}$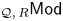
of additive functors from a small preadditive category $\mathcal {Q}$
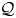satisfying certain conditions to the module category ${_{R}\mathsf {Mod}}$
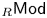over an associative ring $R$
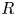, whose homotopy category is the $\mathcal {Q}$
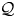-shaped derived category introduced by Holm and Jørgensen. Moreover, we prove that for an arbitrary associative ring $R$
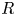, an object in ${_{\mathcal {Q},\,R}\mathsf {Mod}}$
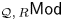is Gorenstein projective (resp., Gorenstein injective, Gorenstein flat, projective coresolving Gorenstein flat) if and only if so is its value on each object of $\mathcal {Q}$
, and hence improve a result by Dell'Ambrogio, Stevenson and Šťovíček.
