We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Simpson [6] showed that every countable model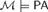 
${\cal M} \models PA$ has an expansion 
$\left( {{\cal M},X} \right) \models P{A^{\rm{*}}}$ that is pointwise definable. A natural question is whether, in general, one can obtain expansions of a nonprime model in which the definable elements coincide with those of the underlying model. Enayat [1] showed that this is impossible by proving that there is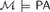 
${\cal M} \models PA$ such that for each undefinable class X of 
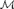${\cal M}$, the expansion 
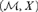$\left( {{\cal M},X} \right)$ is pointwise definable. We call models with this property Enayat models. In this article, we study Enayat models and show that a model of 
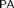$PA$ is Enayat if it is countable, has no proper cofinal submodels and is a conservative extension of all of its elementary cuts. We then show that, for any countable linear order γ, if there is a model 
${\cal M}$ such that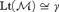 
$Lt\left( {\cal M} \right) \cong \gamma$, then there is an Enayat model 
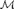${\cal M}$ such that 
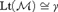$Lt\left( {\cal M} \right) \cong \gamma$.
