We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
For homogeneous polynomials 
$G_1,\ldots ,G_k$ over a finite field, their Dwork complex is defined by Adolphson and Sperber, based on Dwork’s theory. In this article, we will construct an explicit cochain map from the Dwork complex of 
$G_1,\ldots ,G_k$ to the Monsky–Washnitzer complex associated with some affine bundle over the complement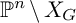 
$\mathbb {P}^n\setminus X_G$ of the common zero 
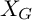$X_G$ of 
$G_1,\ldots ,G_k$, which computes the rigid cohomology of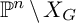 
$\mathbb {P}^n\setminus X_G$. We verify that this cochain map realizes the rigid cohomology of 
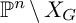$\mathbb {P}^n\setminus X_G$ as a direct summand of the Dwork cohomology of 
$G_1,\ldots ,G_k$. We also verify that the comparison map is compatible with the Frobenius and the Dwork operator defined on both complexes, respectively. Consequently, we extend Katz’s comparison results in [19] for projective hypersurface complements to arbitrary projective complements.
