In order to study integers with few prime factors, the average of 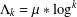 $\unicode[STIX]{x1D6EC}_{k}=\unicode[STIX]{x1D707}\ast \log ^{k}$ has been a central object of research. One of the more important cases,
$\unicode[STIX]{x1D6EC}_{k}=\unicode[STIX]{x1D707}\ast \log ^{k}$ has been a central object of research. One of the more important cases, 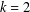 $k=2$, was considered by Selberg [‘An elementary proof of the prime-number theorem’, Ann. of Math. (2)50 (1949), 305–313]. For
$k=2$, was considered by Selberg [‘An elementary proof of the prime-number theorem’, Ann. of Math. (2)50 (1949), 305–313]. For 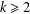 $k\geq 2$, it was studied by Bombieri [‘The asymptotic sieve’, Rend. Accad. Naz. XL (5)1(2) (1975/76), 243–269; (1977)] and later by Friedlander and Iwaniec [‘On Bombieri’s asymptotic sieve’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (4)5(4) (1978), 719–756], as an application of the asymptotic sieve.
$k\geq 2$, it was studied by Bombieri [‘The asymptotic sieve’, Rend. Accad. Naz. XL (5)1(2) (1975/76), 243–269; (1977)] and later by Friedlander and Iwaniec [‘On Bombieri’s asymptotic sieve’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (4)5(4) (1978), 719–756], as an application of the asymptotic sieve.
Let 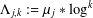 $\unicode[STIX]{x1D6EC}_{j,k}:=\unicode[STIX]{x1D707}_{j}\ast \log ^{k}$, where
$\unicode[STIX]{x1D6EC}_{j,k}:=\unicode[STIX]{x1D707}_{j}\ast \log ^{k}$, where 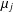 $\unicode[STIX]{x1D707}_{j}$ denotes the Liouville function for
$\unicode[STIX]{x1D707}_{j}$ denotes the Liouville function for 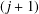 $(j+1)$-free integers, and
$(j+1)$-free integers, and  $0$ otherwise. In this paper we evaluate the average value of
$0$ otherwise. In this paper we evaluate the average value of 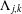 $\unicode[STIX]{x1D6EC}_{j,k}$ in a residue class
$\unicode[STIX]{x1D6EC}_{j,k}$ in a residue class 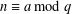 $n\equiv a\text{ mod }q$,
$n\equiv a\text{ mod }q$, 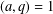 $(a,q)=1$, uniformly on
$(a,q)=1$, uniformly on 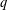 $q$. When
$q$. When 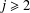 $j\geq 2$, we find that the average value in a residue class differs by a constant factor from the expected value. Moreover, an explicit formula of Weil type for
$j\geq 2$, we find that the average value in a residue class differs by a constant factor from the expected value. Moreover, an explicit formula of Weil type for 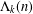 $\unicode[STIX]{x1D6EC}_{k}(n)$ involving the zeros of the Riemann zeta function is derived for an arbitrary compactly supported
$\unicode[STIX]{x1D6EC}_{k}(n)$ involving the zeros of the Riemann zeta function is derived for an arbitrary compactly supported 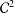 ${\mathcal{C}}^{2}$ function.
${\mathcal{C}}^{2}$ function.