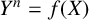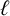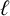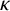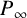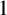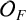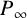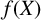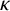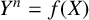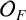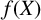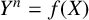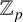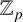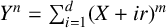Let 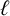 $\ell $ and p be (not necessarily distinct) prime numbers and F be a global function field of characteristic
$\ell $ and p be (not necessarily distinct) prime numbers and F be a global function field of characteristic 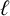 $\ell $ with field of constants
$\ell $ with field of constants 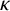 $\kappa $. Assume that there exists a prime
$\kappa $. Assume that there exists a prime 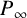 $P_\infty $ of F which has degree
$P_\infty $ of F which has degree 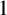 $1$ and let
$1$ and let 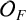 $\mathcal {O}_F$ be the subring of F consisting of functions with no poles away from
$\mathcal {O}_F$ be the subring of F consisting of functions with no poles away from 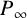 $P_\infty $. Let
$P_\infty $. Let 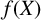 $f(X)$ be a polynomial in X with coefficients in
$f(X)$ be a polynomial in X with coefficients in 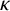 $\kappa $. We study solutions to Diophantine equations of the form
$\kappa $. We study solutions to Diophantine equations of the form 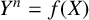 $Y^{n}=f(X)$ which lie in
$Y^{n}=f(X)$ which lie in 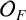 $\mathcal {O}_F$ and, in particular, show that if m and
$\mathcal {O}_F$ and, in particular, show that if m and 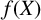 $f(X)$ satisfy additional conditions, then there are no nonconstant solutions. The results apply to the study of solutions to
$f(X)$ satisfy additional conditions, then there are no nonconstant solutions. The results apply to the study of solutions to 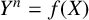 $Y^{n}=f(X)$ in certain rings of integers in
$Y^{n}=f(X)$ in certain rings of integers in 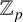 $\mathbb {Z}_{p}$-extensions of F known as constant
$\mathbb {Z}_{p}$-extensions of F known as constant 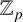 $\mathbb {Z}_p$-extensions. We prove similar results for solutions in the polynomial ring
$\mathbb {Z}_p$-extensions. We prove similar results for solutions in the polynomial ring  $K[T_1, \ldots , T_r]$, where K is any field of characteristic
$K[T_1, \ldots , T_r]$, where K is any field of characteristic  $\ell $, showing that the only solutions must lie in K. We apply our methods to study solutions of Diophantine equations of the form
$\ell $, showing that the only solutions must lie in K. We apply our methods to study solutions of Diophantine equations of the form 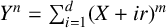 $Y^n=\sum _{i=1}^d (X+ir)^m$, where
$Y^n=\sum _{i=1}^d (X+ir)^m$, where  $m,n, d\geq 2$ are integers.
$m,n, d\geq 2$ are integers.
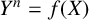 $Y^n=f(X)$ OVER FUNCTION FIELDS
$Y^n=f(X)$ OVER FUNCTION FIELDS