We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We give an asymptotic formula for correlations where 
$$\begin{eqnarray}\mathop{\sum }_{n\leqslant x}f_{1}(P_{1}(n))f_{2}(P_{2}(n))\cdots f_{m}(P_{m}(n)),\end{eqnarray}$$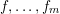
$f,\ldots ,f_{m}$ are bounded ‘pretentious’ multiplicative functions, under certain natural hypotheses. We then deduce several desirable consequences. First, we characterize all multiplicative functions 
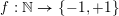$f:\mathbb{N}\rightarrow \{-1,+1\}$ with bounded partial sums. This answers a question of Erdős from 
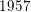$1957$ in the form conjectured by Tao. Second, we show that if the average of the first divided difference of the multiplicative function is zero, then either 
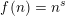$f(n)=n^{s}$ for 
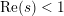$\operatorname{Re}(s)<1$ or 
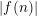$|f(n)|$ is small on average. This settles an old conjecture of Kátai. Third, we apply our theorem to count the number of representations of 
$n=a+b$, where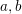 
$a,b$ belong to some multiplicative subsets of 
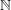$\mathbb{N}$. This gives a new ‘circle method-free’ proof of a result of Brüdern.
