This paper examines the infinitely high dam with seasonal (periodic) Lévy input under the unit release rule. We show that a periodic limiting distribution of dam content exists whenever the mean input over a seasonal cycle is less than 1. The Laplace transform of dam content at a finite time and the Laplace transform of the periodic limiting distribution are derived in terms of the probability of an empty dam. Necessary and sufficient conditions for the periodic limiting distribution to have finite moments are given. Convergence rates to the periodic limiting distribution are obtained from the moment results. Our methods of analysis lean heavily on the coupling method and a stochastic monotonicity result.

This article attempts to provide a historical perspective of the author's involvement in applied probability. Several research problems in this area are described, and three organizational experiences of importance to the author outlined. After a brief account of the development of the Applied Probability journals, the article concludes with some philosophical remarks.

A construction is given of a process in which X(t) represents the content at time t of a dam whose cumulative input process is a Lévy process with measure v and whose release rate at time t is r(X(t)). It is assumed only that r(0) = 0 and that r is strictly positive and left-continuous with strictly positive finite right limits on (0,∞). The sample-paths of X are shown to satisfy the storage equation

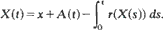
The process X is analyzed using renewal theory and stochastic comparison techniques, and necessary and sufficient conditions are found in terms of v and r for X to have a stationary distributionπ. These generalize previous results which were obtained under the assumption that v is finite. Conditions for Πto have an atom at 0 are considered in some detail, and related results on the positivity of the expected occupation time of level 0 are given.

Necessary and sufficient conditions for the existence of Πare expressed in terms of the existence of non-negative integrable solutions of certain integral equations and conditions are given under which such solutions are necessarily stationary densities for X. A simple sufficient condition for X to have a stationary distribution is found in terms of 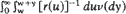and in the case when r is non-decreasing the condition is shown to be also necessary. Finally some examples are considered; these show that the results described above unify various known conditions in special cases, and confirm several conjectures in the related literature.

Conditions are derived under which a probability measure on the Borel subsets of [0, ∞) is a stationary distribution for the content {Xt} of an infinite dam whose cumulative input {At} is a pure-jump Lévy process and whose release rate is a non-decreasing continuous function r(·) of the content. The conditions are used to find stationary distributions in a number of special cases, in particular when and when r(x) = xα and {At} is stable with index β ∊ (0, 1). In general if EAt, < ∞ and r(0 +) > 0 it is shown that the condition sup r(x)>EA1 is necessary and sufficient for a stationary distribution to exist, a stationary distribution being found explicitly when the conditions are satisfied. If sup r(x)>EA1 it is shown that there is at most one stationary distribution and that if there is one then it is the limiting distribution of {Xt} as t → ∞. For {At} stable with index β and r(x) = xα, α + β = 1, we show also that complementing results of Brockwell and Chung for the zero-set of {Xt} in the cases α + β < 1 and α + β > 1. We conclude with a brief treatment of the finite dam, regarded as a limiting case of infinite dams with suitably chosen release functions.