We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study D0L power series over commutative semirings. We show that a sequence(cn )n≥0 of nonzero elements of a field A is the coefficientsequence of a D0L power series if and only if there exist a positive integerk and integers βi for 1 ≤ i ≤ k such that $c_{n+k}=c_{n+k-1}^{\beta_1}c_{n+k-2}^{\beta_2}\ldots c_n^{\beta_k}$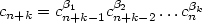 
for alln ≥ 0. As a consequence we solve the equivalence problem of D0L powerseries over computable fields.
