We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The Lusternik–Schnirelmann category of the quaternionic Grassmannian
is known to be k(n − k). In this paper we show that this result can be deduced from Morse theory.
We explicitly describe the best approximation in geodesic submanifolds of positive definite matrices obtained from involutive congruence transformations on the Cartan-Hadamard manifold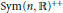 
$\text{Sym(}n\text{,}\,\mathbb{R}{{\text{)}}^{++}}$ of positive definite matrices. An explicit calculation for the minimal distance function from the geodesic submanifold 
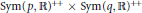$\text{Sym(}p\text{,}\,\mathbb{R}{{\text{)}}^{++}}\,\times \,\text{Sym(}q\text{,}\,\mathbb{R}{{\text{)}}^{++}}$ block diagonally embedded in 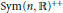$\text{Sym(}n\text{,}\,\mathbb{R}{{\text{)}}^{++}}$ is given in terms of metric and spectral geometric means, Cayley transform, and Schur complements of positive definite matrices when 
$p\,\le \,2$ or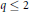 
$q\,\le \,2$.
