This study investigates experimentally the pressure fluctuations of liquids in a column under short-time acceleration. It demonstrates that the Strouhal number  $St=L/(c\,\Delta t)$, where
$St=L/(c\,\Delta t)$, where 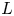 $L$,
$L$, 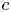 $c$ and
$c$ and 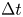 $\Delta t$ are the liquid column length, speed of sound, and acceleration duration, respectively, provides a measure of the pressure fluctuations for intermediate
$\Delta t$ are the liquid column length, speed of sound, and acceleration duration, respectively, provides a measure of the pressure fluctuations for intermediate 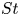 $St$ values. On the one hand, the incompressible fluid theory implies that the magnitude of the averaged pressure fluctuation
$St$ values. On the one hand, the incompressible fluid theory implies that the magnitude of the averaged pressure fluctuation 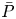 $\bar {P}$ becomes negligible for
$\bar {P}$ becomes negligible for  $St\ll 1$. On the other hand, the water hammer theory predicts that the pressure tends to
$St\ll 1$. On the other hand, the water hammer theory predicts that the pressure tends to  $\rho cu_0$ (where
$\rho cu_0$ (where  $u_0$ is the change in the liquid velocity) for
$u_0$ is the change in the liquid velocity) for 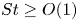 $St\geq O(1)$. For intermediate
$St\geq O(1)$. For intermediate 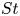 $St$ values, there is no consensus on the value of
$St$ values, there is no consensus on the value of 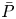 $\bar {P}$. In our experiments,
$\bar {P}$. In our experiments, 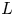 $L$,
$L$, 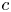 $c$ and
$c$ and 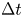 $\Delta t$ are varied so that
$\Delta t$ are varied so that  $0.02 \leq St \leq 2.2$. The results suggest that the incompressible fluid theory holds only up to
$0.02 \leq St \leq 2.2$. The results suggest that the incompressible fluid theory holds only up to  $St\sim 0.2$, and that
$St\sim 0.2$, and that 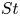 $St$ governs the pressure fluctuations under different experimental conditions for higher
$St$ governs the pressure fluctuations under different experimental conditions for higher 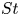 $St$ values. The data relating to a hydrogel also tend to collapse to a unified trend. The inception of cavitation in the liquid starts at
$St$ values. The data relating to a hydrogel also tend to collapse to a unified trend. The inception of cavitation in the liquid starts at  $St\sim 0.2$ for various
$St\sim 0.2$ for various  $\Delta t$, indicating that the liquid pressure goes lower than the liquid vapour pressure. To understand this mechanism, we employ a one-dimensional wave propagation model with a pressure wavefront of finite thickness that scales with
$\Delta t$, indicating that the liquid pressure goes lower than the liquid vapour pressure. To understand this mechanism, we employ a one-dimensional wave propagation model with a pressure wavefront of finite thickness that scales with  $\Delta t$. The model provides a reasonable description of the experimental results as a function of
$\Delta t$. The model provides a reasonable description of the experimental results as a function of 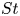 $St$.
$St$.