We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The purpose of this paper is to characterize positive measure 
$\mu$ on the unit disk such that the analytic Morrey space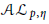 
$\mathcal{A}{{\mathcal{L}}_{p,\eta }}$ is boundedly and compactly embedded to the tent space
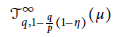$$\mathcal{J}_{q,1-\frac{q}{p}\left( 1-\eta \right)}^{\infty }\left( \mu \right)$$
for the case 
$1\,\le \,q\,\le \,p\,<\,\infty$ respectively. As an application, these results are used to establish the boundedness and compactness of integral operators and multipliers between analytic Morrey spaces.
