Let R be a ring and let 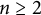$n\ge 2$. We discuss the question of whether every element in the matrix ring $M_n(R)$ is a product of (additive) commutators $[x,y]=xy-yx$, for $x,y\in M_n(R)$. An example showing that this does not always hold, even when R is commutative, is provided. If, however, R has Bass stable rank one, then under various additional conditions every element in 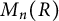$M_n(R)$ is a product of three commutators. Further, if R is a division ring with infinite center, then every element in $M_n(R)$ is a product of two commutators. If R is a field and $a\in M_n(R)$, then every element in $M_n(R)$ is a sum of elements of the form $[a,x][a,y]$ with $x,y\in M_n(R)$ if and only if the degree of the minimal polynomial of a is greater than $2$.

Let $K$ denote a compact real symmetric subset of $\mathbb{C}$ and let ${{A}_{\mathbb{R}}}\left( K \right)$ denote the real Banach algebra of all real symmetric continuous functions on $K$ that are analytic in the interior ${{K}^{\circ }}$ of $K$, endowed with the supremum norm. We characterize all unimodular pairs $\left( f,\,g \right)$ in ${{A}_{\mathbb{R}}}{{\left( K \right)}^{2}}$ which are reducible. In addition, for an arbitrary compact $K$ in $\mathbb{C}$, we give a new proof (not relying on Banach algebra theory or elementary stable rank techniques) of the fact that the Bass stable rank of $A\left( K \right)$ is 1. Finally, we also characterize all compact real symmetric sets $K$ such that ${{A}_{\mathbb{R}}}\left( K \right)$, respectively ${{C}_{\mathbb{R}}}\left( K \right)$, has Bass stable rank 1.