Motivated by new examples of functional Banach spaces over the unit disk, arising as the symbol spaces in the study of random analytic functions, for which the monomials $\{z^n\}_{n\geq 0}$ exhibit features of an unconditional basis yet they often don’t even form a Schauder basis, we introduce a notion called solid basis for Banach spaces and p-Banach spaces and study its properties. Besides justifying the rich existence of solid bases, we study their relationship with unconditional bases, the weak-star convergence of Taylor polynomials, the problem of a solid span and the curious roles played by c0. The two features of this work are as follows: (1) during the process, we are led to revisit the axioms satisfied by a typical Banach space of analytic functions over the unit disk, leading to a notion of $\mathcal{X}^\mathrm{max}$ (and $\mathcal{X}^\mathrm{min}$), as well as a number of related functorial constructions, which are of independent interests; (2) the main interests of solid basis lie in the case of non-separable (p-)Banach spaces, such as BMOA and the Bloch space instead of VMOA and the little Bloch space.

We introduce and study some new function spaces on Riemann surfaces. For certain parameter values these spaces coincide with the classical Dirichlet space, $\text{BMOA}$, or the recently defined ${{\text{Q}}_{p}}$ space. We establish inclusion relations that generalize earlier known inclusions between the above-mentioned spaces.

The ${{Q}_{p}}$ spaces coincide with the Bloch space for $p\,>\,1$ and are subspaces of $\text{BMOA}$ for $0\,<\,p\,\le \,1$. We obtain lower and upper estimates for the essential norm of a composition operator from the Bloch space into ${{Q}_{p}}$, in particular from the Bloch space into $\text{BMOA}$.

A holomorphic map ψ of the unit disk ito itself induces an operator Cψ on holomorphic functions by composition. We characterize bounded and compact composition operators Cψ on Qp spaces, which coincide with the BMOA for p = 1 and Bloch spaces for p > 1. We also give boundedness and compactness characterizations of Cψ from analytic function space X to Qp spaces, X = Dirichlet space D, Bloch space B or B0 = {f: f′ ∈ H∞}.

In this paper we prove a number of results on Cauchy transforms of generalized type given by Borel measures supported on the class of analytic functions mapping the unit disc into the unit disk. We also give a BMOA characterization using these families.

Let 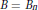$B\,=\,{{B}_{n}}$ be the open unit ball of 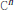${{C}^{n}}$ with volume measure $v$, $U\,=\,{{B}_{1}}$ and 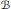$B$ be the Bloch space on 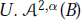$U.\,{{\mathcal{A}}^{2,\alpha }}(B)$, 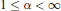$1\,\le \,\alpha \,<\infty $, is defined as the set of holomorphic 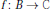$f\,:\,B\,\to \,C$ for which

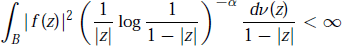$$\int_{B\,}{{{\left| f(z) \right|}^{2}}}{{\left( \frac{1}{\left| z \right|}\,\log \frac{1}{1\,-\left| z \right|} \right)}^{-\alpha }}\,\frac{dv(z)}{1\,-\,\left| z \right|}\,<\,\infty $$

if 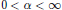$0\,<\,\alpha \,<\infty $ and 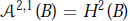${{\mathcal{A}}^{2,1}}(B)\,=\,{{H}^{2}}(B)$, the Hardy space. Our objective of this note is to characterize, in terms of the Bergman distance, those holomorphic 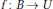$f\,:\,B\,\to \,U$ for which the composition operator 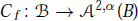${{C}_{f}}\,:\,B\,\to \,{{\mathcal{A}}^{2,\alpha }}(B)$ defined by ${{C}_{f}}(g)=g\,\text{o}\,f\text{,}\,g\in B$, is bounded. Our result has a corollary that characterize the set of analytic functions of bounded mean oscillation with respect to the Bergman metric.

We show that the multiplier space , where X is BMOA, VMOA, B, B0 or disk algebra A. We give the multipliers from , we also give the multipliers from , C0, BMOA, and Hp.