We give explicit formulas witnessing IP, IP$_{\!n}$, or TP2 in fields with Artin–Schreier extensions. We use them to control p-extensions of mixed characteristic henselian valued fields, allowing us most notably to generalize to the NIP$_{\!n}$ context one way of Anscombe–Jahnke’s classification of NIP henselian valued fields. As a corollary, we obtain that NIP$_{\!n}$ henselian valued fields with NIP residue field are NIP. We also discuss tameness results for NTP2 henselian valued fields.

We study the Galois module structure of the class groups of the Artin–Schreier extensions K over k of extension degree p, where 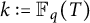$k:={\mathbb F}_q(T)$ is the rational function field and p is a prime number. The structure of the p-part $Cl_K(p)$ of the ideal class group of K as a finite G-module is determined by the invariant 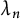${\lambda }_n$, where 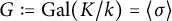$G:=\operatorname {\mathrm {Gal}}(K/k)=\langle {\sigma } \rangle $ is the Galois group of K over k, and ${\lambda }_n = \dim _{{\mathbb F}_p}(Cl_K(p)^{({\sigma }-1)^{n-1}}/Cl_K(p)^{({\sigma }-1)^{n}})$. We find infinite families of the Artin–Schreier extensions over k whose ideal class groups have guaranteed prescribed ${\lambda }_n$-rank for 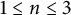$1 \leq n \leq 3$. We find an algorithm for computing 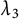${\lambda }_3$-rank of 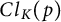$Cl_K(p)$. 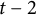Using this algorithm, for a given integer $t \ge 2$, we get infinite families of the Artin–Schreier extensions over k whose ${\lambda }_1$-rank is t, ${\lambda }_2$-rank is $t-1$, and ${\lambda }_3$-rank is $t-2$. In particular, in the case where $p=2$, for a given positive integer $t \ge 2$, we obtain an infinite family of the Artin–Schreier quadratic extensions over k whose $2$-class group rank (resp. $2^2$-class group rank and 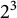$2^3$-class group rank) is exactly t (resp. $t-1$ and $t-2$). Furthermore, we also obtain a similar result on the 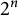$2^n$-ranks of the divisor class groups of the Artin–Schreier quadratic extensions over k.

We study the McKay correspondence for representations of the cyclic group of order $p$ in characteristic $p$. The main tool is the motivic integration generalized to quotient stacks associated to representations. Our version of the change of variables formula leads to an explicit computation of the stringy invariant of the quotient variety. A consequence is that a crepant resolution of the quotient variety (if any) has topological Euler characteristic $p$ as in the tame case. Also, we link a crepant resolution with a count of Artin–Schreier extensions of the power series field with respect to weights determined by ramification jumps and the representation.