If 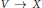 $V\,\to \,X$ is a vector bundle of fiber dimension
$V\,\to \,X$ is a vector bundle of fiber dimension 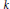 $k$ and
$k$ and 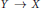 $Y\,\to \,X$ is a finite sheeted covering map of degree
$Y\,\to \,X$ is a finite sheeted covering map of degree 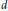 $d$, the implications for the Euler class
$d$, the implications for the Euler class 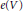 $e(V)$ in
$e(V)$ in 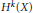 ${{H}^{k}}(X)$ of
${{H}^{k}}(X)$ of 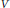 $V$ implied by the existence of an embedding
$V$ implied by the existence of an embedding 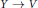 $Y\,\to \,V$ lifting the covering map are explored. In particular it is proved that
$Y\,\to \,V$ lifting the covering map are explored. In particular it is proved that  $d{{d}^{\prime }}\text{e(V)}\text{=}\text{0}$ where
$d{{d}^{\prime }}\text{e(V)}\text{=}\text{0}$ where 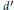 ${{d}^{\prime }}$ is a certain divisor of
${{d}^{\prime }}$ is a certain divisor of 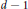 $d\,-\,1$, and often
$d\,-\,1$, and often 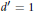 ${{d}^{\prime }}=1$.
${{d}^{\prime }}=1$.