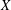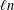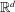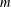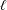Holmsen, Kynčl and Valculescu recently conjectured that if a finite set $X$ with $\ell n$ points in $\mathbb{R}^{d}$ that is colored by $m$ different colors can be partitioned into $n$ subsets of $\ell$ points each, such that each subset contains points of at least 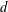$d$ different colors, then there exists such a partition of 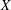$X$ with the additional property that the convex hulls of the $n$ subsets are pairwise disjoint.

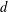We prove a continuous analogue of this conjecture, generalized so that each subset contains points of at least $c$ different colors, where we also allow $c$ to be greater than $d$. Furthermore, we give lower bounds on the fraction of the points each of the subsets contains from $c$ different colors. For example, when 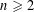$n\geqslant 2$, $d\geqslant 2$, 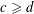$c\geqslant d$ with 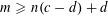$m\geqslant n(c-d)+d$ are integers, and 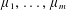$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{m}$ are 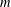$m$ positive finite absolutely continuous measures on 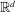$\mathbb{R}^{d}$, we prove that there exists a partition of 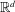$\mathbb{R}^{d}$ into $n$ convex pieces which equiparts the measures 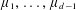$\unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{d-1}$, and in addition every piece of the partition has positive measure with respect to at least $c$ of the measures $\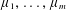unicode[STIX]{x1D707}_{1},\ldots ,\unicode[STIX]{x1D707}_{m}$.

We consider the cohomology of Mackey functors for infinite groups and define the Mackey-cohomological dimension ${\rm cd}_{{\mathfrak M}} G$ of a group $G$. We will relate this dimension to other cohomological dimensions such as the Bredon-cohomological dimension ${\rm cd}_{{\mathfrak F}}G$ and the relative cohomological dimension ${{\mathfrak F}}\text{-}{\rm cd} G$. In particular, we show that for virtually torsion free groups the Mackey-cohomological dimension is equal to both ${{\mathfrak F}}\text{-}{\rm cd} G$ and the virtual cohomological dimension.