Consider the wreath product  $H\,\wr \,G$, where
$H\,\wr \,G$, where 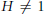 $H\,\ne \,1$ is finite and
$H\,\ne \,1$ is finite and  $G$ is finitely generated. We show that the Assouad–Nagata dimension
$G$ is finitely generated. We show that the Assouad–Nagata dimension 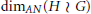 ${{\dim}_{AN}}\left( H\,\wr \,G \right)$ of
${{\dim}_{AN}}\left( H\,\wr \,G \right)$ of  $H\,\wr \,G$ depends on the growth of
$H\,\wr \,G$ depends on the growth of  $G$ as follows: if the growth of
$G$ as follows: if the growth of  $G$ is not bounded by a linear function, then
$G$ is not bounded by a linear function, then 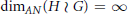 ${{\dim}_{AN}}\left( H\,\wr \,G \right)\,=\,\infty$; otherwise
${{\dim}_{AN}}\left( H\,\wr \,G \right)\,=\,\infty$; otherwise  ${{\dim}_{AN}}\left( H\,\wr \,G \right)\,=\,{{\dim}_{AN}}\left( G \right)\,\le \,1$.
${{\dim}_{AN}}\left( H\,\wr \,G \right)\,=\,{{\dim}_{AN}}\left( G \right)\,\le \,1$.