In this paper, we give a new proof of the Onofri-type inequality
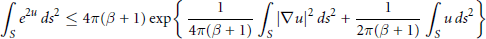 $$\int_{S}{{{e}^{2u}}\,d{{s}^{2}}\,\le \,4\pi (\beta \,+\,1)\,\text{exp}}\left\{ \frac{1}{4\pi (\beta \,+\,1)}{{\int_{S}{\left| \nabla u \right|}}^{2}}\,d{{s}^{2}}\,+\,\frac{1}{2\pi (\beta \,+\,1)}\,\int_{S}{u\,d{{s}^{2}}} \right\}$$
$$\int_{S}{{{e}^{2u}}\,d{{s}^{2}}\,\le \,4\pi (\beta \,+\,1)\,\text{exp}}\left\{ \frac{1}{4\pi (\beta \,+\,1)}{{\int_{S}{\left| \nabla u \right|}}^{2}}\,d{{s}^{2}}\,+\,\frac{1}{2\pi (\beta \,+\,1)}\,\int_{S}{u\,d{{s}^{2}}} \right\}$$
on the sphere  $S$ with Gaussian curvature 1 and with conical singularities divisor
$S$ with Gaussian curvature 1 and with conical singularities divisor 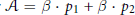 $\mathcal{A}\,=\,\beta \,\cdot \,{{p}_{1}}\,+\,\beta \,\cdot \,{{p}_{2}}$ for
$\mathcal{A}\,=\,\beta \,\cdot \,{{p}_{1}}\,+\,\beta \,\cdot \,{{p}_{2}}$ for  $\beta \in \,(-1,\,0)$; here
$\beta \in \,(-1,\,0)$; here 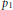 ${{p}_{1}}$ and
${{p}_{1}}$ and 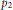 ${{p}_{2}}$ are antipodal.
${{p}_{2}}$ are antipodal.
 4
4