By 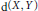 $\text{d(X,Y)}$ we denote the (multiplicative) Banach–Mazur distance between two normed spaces
$\text{d(X,Y)}$ we denote the (multiplicative) Banach–Mazur distance between two normed spaces  $X$ and
$X$ and  $Y$. Let
$Y$. Let  $X$ be an
$X$ be an  $n$-dimensional normed space with
$n$-dimensional normed space with 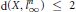 $\text{d(X,}\,l_{\infty }^{n}\text{)}\,\le \,\text{2}$, where
$\text{d(X,}\,l_{\infty }^{n}\text{)}\,\le \,\text{2}$, where 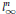 $l_{\infty }^{n}$ stands for
$l_{\infty }^{n}$ stands for 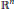 ${{\mathbb{R}}^{n}}$ endowed with the norm
${{\mathbb{R}}^{n}}$ endowed with the norm 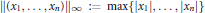 $\parallel ({{x}_{1}},\,.\,.\,.\,,\,{{x}_{n}}){{\parallel }_{\infty }}\,:=\,\max \{|{{x}_{1}}|,\,.\,.\,.\,,\,|{{x}_{n}}|\}$. Then every metric space
$\parallel ({{x}_{1}},\,.\,.\,.\,,\,{{x}_{n}}){{\parallel }_{\infty }}\,:=\,\max \{|{{x}_{1}}|,\,.\,.\,.\,,\,|{{x}_{n}}|\}$. Then every metric space 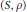 $(S,\,\rho )$ of cardinality
$(S,\,\rho )$ of cardinality  $n+1$ with norm
$n+1$ with norm  $\rho $ satisfying the condition
$\rho $ satisfying the condition  $\max D/\min D\,\le \,2/\,\text{d(}X,\,l_{\infty }^{n}\text{)}$ for
$\max D/\min D\,\le \,2/\,\text{d(}X,\,l_{\infty }^{n}\text{)}$ for 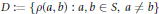 $D\,:=\,\{\rho (a,\,b)\,:\,a,\,b\,\in \,S,\,a\,\ne \,b\}$ can be isometrically embedded into
$D\,:=\,\{\rho (a,\,b)\,:\,a,\,b\,\in \,S,\,a\,\ne \,b\}$ can be isometrically embedded into  $X$.
$X$.