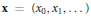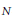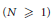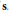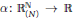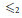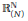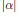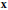Let 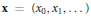 $\mathbf{x}\,=\,\left( {{x}_{0}},\,{{x}_{1}},.\,.\,. \right)$ be a
$\mathbf{x}\,=\,\left( {{x}_{0}},\,{{x}_{1}},.\,.\,. \right)$ be a 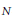 $N$-periodic sequence of integers
$N$-periodic sequence of integers 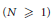 $\left( N\,\ge \,1 \right)$, and
$\left( N\,\ge \,1 \right)$, and 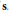 $\mathbf{s}$ a sturmian sequence with the same barycenter (and also
$\mathbf{s}$ a sturmian sequence with the same barycenter (and also 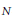 $N$-periodic, consequently). It is shown that, for affine functions
$N$-periodic, consequently). It is shown that, for affine functions 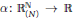 $\alpha :\,\mathbb{R}_{(N)}^{\mathbb{N}}\,\to \,\mathbb{R}$ which are increasing relatively to some order
$\alpha :\,\mathbb{R}_{(N)}^{\mathbb{N}}\,\to \,\mathbb{R}$ which are increasing relatively to some order 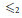 ${{\le }_{2}}$ on
${{\le }_{2}}$ on 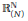 $\mathbb{R}_{(N)}^{\mathbb{R}}$ (the space of all
$\mathbb{R}_{(N)}^{\mathbb{R}}$ (the space of all 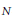 $N$-periodic sequences), the average of
$N$-periodic sequences), the average of 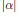 $\left| \alpha \right|$ on the orbit of
$\left| \alpha \right|$ on the orbit of 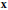 $\mathbf{x}$ is greater than its average on the orbit of
$\mathbf{x}$ is greater than its average on the orbit of 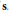 $\mathbf{s}$.
$\mathbf{s}$.