Let 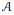 $\mathcal{A}$ be a
$\mathcal{A}$ be a 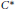 ${{C}^{*}}$-algebra and
${{C}^{*}}$-algebra and  $E$ be a Banach space with the Radon-Nikodym property. We prove that if
$E$ be a Banach space with the Radon-Nikodym property. We prove that if 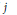 $j$ is an embedding of
$j$ is an embedding of  $E$ into an injective Banach space then for every absolutely summing operator
$E$ into an injective Banach space then for every absolutely summing operator 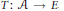 $T:\,\mathcal{A}\,\to \,E$, the composition
$T:\,\mathcal{A}\,\to \,E$, the composition 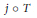 $j\,\circ \,T$ factors through a diagonal operator from
$j\,\circ \,T$ factors through a diagonal operator from 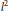 ${{l}^{2}}$ into
${{l}^{2}}$ into 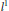 ${{l}^{1}}$. In particular,
${{l}^{1}}$. In particular, 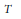 $T$ factors through a Banach space with the Schur property. Similarly, we prove that for
$T$ factors through a Banach space with the Schur property. Similarly, we prove that for 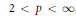 $2\,<\,p\,<\,\infty $, any absolutely summing operator from
$2\,<\,p\,<\,\infty $, any absolutely summing operator from 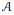 $\mathcal{A}$ into
$\mathcal{A}$ into  $E$ factors through a diagonal operator from
$E$ factors through a diagonal operator from 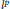 ${{l}^{p}}$ into
${{l}^{p}}$ into 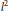 ${{l}^{2}}$.
${{l}^{2}}$.
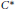 ${{C}^{*}}$-Algebras and Factorization Through Diagonal Operators
${{C}^{*}}$-Algebras and Factorization Through Diagonal Operators