We discuss representations of product systems (of $W^*$-correspondences) over the semigroup $\mathbb{Z}^n_+$ and show that, under certain pureness and Szegö positivity conditions, a completely contractive representation can be dilated to an isometric representation. For $n=1,2$ this is known to hold in general (without assuming the conditions), but for $n\geq 3$, it does not hold in general (as is known for the special case of isometric dilations of a tuple of commuting contractions). Restricting to the case of tuples of commuting contractions, our result reduces to a result of Barik, Das, Haria, and Sarkar (Isometric dilations and von Neumann inequality for a class of tuples in the polydisc. Trans. Amer. Math. Soc. 372 (2019), 1429–1450). Our dilation is explicitly constructed, and we present some applications.

The goal of this paper is to show that the theory of curvature invariant, as introduced by Arveson, admits a natural extension to the framework of ${\mathcal U}$-twisted polyballs $B^{\mathcal U}({\mathcal H})$ which consist of k-tuples $(A_1,\ldots, A_k)$ of row contractions $A_i=(A_{i,1},\ldots, A_{i,n_i})$ satisfying certain ${\mathcal U}$-commutation relations with respect to a set ${\mathcal U}$ of unitary commuting operators on a Hilbert space ${\mathcal H}$. Throughout this paper, we will be concerned with the curvature of the elements $A\in B^{\mathcal U}({\mathcal H})$ with positive trace class defect operator $\Delta_A(I)$. We prove the existence of the curvature invariant and present some of its basic properties. A distinguished role as a universal model among the pure elements in ${\mathcal U}$-twisted polyballs is played by the standard $I\otimes{\mathcal U}$-twisted multi-shift S acting on $\ell^2({\mathbb F}_{n_1}^+\times\cdots\times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$. The curvature invariant $\mathrm{curv} (A)$ can be any non-negative real number and measures the amount by which A deviates from the universal model S. Special attention is given to the $I\otimes {\mathcal U}$-twisted multi-shift S and the invariant subspaces (co-invariant) under S and $I\otimes {\mathcal U}$, due to the fact that any pure element $A\in B^{\mathcal U}({\mathcal H})$ with $\Delta_A(I)\geq 0$ is the compression of S to such a co-invariant subspace.

For commuting contractions $T_1,\dots,T_n$ acting on a Hilbert space 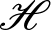$\mathscr{H}$ with 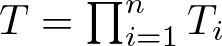$T=\prod_{i=1}^n T_i$, we find a necessary and sufficient condition such that $(T_1,\dots,T_n)$ dilates to a commuting tuple of isometries $(V_1,\dots,V_n)$ on the minimal isometric dilation space of T with 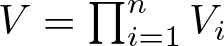$V=\prod_{i=1}^nV_i$ being the minimal isometric dilation of T. This isometric dilation provides a commutant lifting of $(T_1, \dots, T_n)$ on the minimal isometric dilation space of T. We construct both Schäffer and Sz. Nagy–Foias-type isometric dilations for $(T_1,\dots,T_n)$ on the minimal dilation spaces of T. Also, a different dilation is constructed when the product T is a 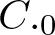$C._0$ contraction, that is, ${T^*}^n \rightarrow 0$ as 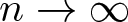$n \rightarrow \infty$. As a consequence of these dilation theorems, we obtain different functional models for $(T_1,\dots,T_n)$ in terms of multiplication operators on vectorial Hardy spaces. One notable fact about our models is that the multipliers are all analytic functions in one variable. The dilation when T is a 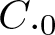$C._0$ contraction leads to a conditional factorization of T. Several examples have been constructed.

Using probabilistic tools, we prove that any weak* continuous semigroup $(T_t)_{t \geqslant 0}$ of self-adjoint unital completely positive measurable Schur multipliers acting on the space $\mathrm {B}({\mathrm {L}}^2(X))$ of bounded operators on the Hilbert space ${\mathrm {L}}^2(X)$, where X is a suitable measure space, can be dilated by a weak* continuous group of Markov $*$-automorphisms on a bigger von Neumann algebra. We also construct a Markov dilation of these semigroups. Our results imply the boundedness of the McIntosh’s ${\mathrm {H}}^\infty $ functional calculus of the generators of these semigroups on the associated Schatten spaces and some interpolation results connected to ${\mathrm {BMO}}$-spaces. We also give an answer to a question of Steen, Todorov, and Turowska on completely positive continuous Schur multipliers.

The aim of this paper is to develop an approach to obtain self-adjoint extensions of symmetric operators acting on anti-dual pairs. The main advantage of such a result is that it can be applied for structures not carrying a Hilbert space structure or a normable topology. In fact, we will show how hermitian extensions of linear functionals of involutive algebras can be governed by means of their induced operators. As an operator theoretic application, we provide a direct generalization of Parrott’s theorem on contractive completion of 2 by 2 block operator-valued matrices. To exhibit the applicability in noncommutative integration, we characterize hermitian extendibility of symmetric functionals defined on a left ideal of a $C^{\ast }$-algebra.

Let 𝔻n be the open unit polydisc in ℂn, $n \ges 1$, and let H2(𝔻n) be the Hardy space over 𝔻n. For $n\ges 3$, we show that if θ ∈ H∞(𝔻n) is an inner function, then the n-tuple of commuting operators $(C_{z_1}, \ldots , C_{z_n})$ on the Beurling type quotient module ${\cal Q}_{\theta }$ is not essentially normal, where

$${\rm {\cal Q}}_\theta = H^2({\rm {\open D}}^n)/\theta H^2({\rm {\open D}}^n)\quad {\rm and}\quad C_{z_j} = P_{{\rm {\cal Q}}_\theta }M_{z_j}\vert_{{\rm {\cal Q}}_\theta }\quad (j = 1, \ldots ,n).$$

We obtain intertwining dilation theorems for non-commutative regular domains 𝒟f and non-commutative varieties 𝒱J in B(𝓗)n, which generalize Sarason and Szőkefalvi-Nagy and Foiaş's commutant lifting theorem for commuting contractions. We present several applications including a new proof for the commutant lifting theorem for pure elements in the domain 𝒟f (respectively, variety 𝒱J ) as well as a Schur-type representation for the unit ball of the Hardy algebra associated with the variety 𝒱J. We provide Andô-type dilations and inequalities for bi-domains 𝒟f ×c 𝒟g consisting of all pairs (X,Y ) of tuples X := (X1,…, Xn1) ∊ 𝒟f and Y := (Y1,…, Yn2) ∊ 𝒟g that commute, i.e. each entry of X commutes with each entry of Y . The results are new, even when n1 = n2 = 1. In this particular case, we obtain extensions of Andô's results and Agler and McCarthy's inequality for commuting contractions to larger classes of commuting operators. All the results are extended to bi-varieties 𝒱J1×c 𝒱J2, where 𝒱J1 and 𝒱J2 are non-commutative varieties generated by weak-operator-topology-closed two-sided ideals in non-commutative Hardy algebras. The commutative case and the matrix case when n1 = n2 = 1 are also discussed.

A commuting family of subnormal operators need not have a commuting normal extension. We study when a representation of an abelian semigroup can be extended to a normal representation, and show that it suffices to extend the set of generators to commuting normals. We also extend a result due to Athavale to representations on abelian lattice ordered semigroups.

Let $S$ be the semigroup $S=\sum\nolimits_{i=1}^{\oplus k}{{{S}_{i}}}$, where for each $i\in I,{{S}_{i}}$ is a countable subsemigroup of the additive semigroup ${{\mathbb{R}}_{+}}$ containing 0. We consider representations of $S$ as contractions ${{\left\{ {{T}_{s}} \right\}}_{s\in S}}$ on a Hilbert space with the Nica-covariance property: $T_{s}^{*}{{T}_{t}}={{T}_{t}}T_{s}^{*}$ whenever $t\wedge s=0$. We show that all such representations have a unique minimal isometric Nica-covariant dilation.

This result is used to help analyse the nonself-adjoint semicrossed product algebras formed from Nica-covariant representations of the action of $S$ on an operator algebra $\mathcal{A}$ by completely contractive endomorphisms. We conclude by calculating the ${{C}^{*}}$-envelope of the isometric nonself-adjoint semicrossed product algebra (in the sense of Kakariadis and Katsoulis).

We define the class of weakly approximately divisible unital ${C}^{\ast } $-algebras and show that this class is closed under direct sums, direct limits, any tensor product with any ${C}^{\ast } $-algebra, and quotients. A nuclear ${C}^{\ast } $-algebra is weakly approximately divisible if and only if it has no finite-dimensional representations. We also show that Pisier’s similarity degree of a weakly approximately divisible ${C}^{\ast } $-algebra is at most five.

In this paper we consider the following ‘Toeplitz completion’ problem: Complete the unspecified analytic Toeplitz entries of the partial block Toeplitz matrix

$ \begin{linenomath} A:=\begin{bmatrix} T_{\overline\psi_1}& ?\\[4pt] \T_{\overline\psi_2} \end{bmatrix} \end{linenomath} $

In this paper we propose a new technical tool for analyzing representations of Hilbert ${{C}^{*}}$- product systems. Using this tool, we give a new proof that every doubly commuting representation over ${{\mathbb{N}}^{k}}$ has a regular isometric dilation, and we also prove sufficient conditions for the existence of a regular isometric dilation of representations over more general subsemigroups of $\mathbb{R}_{+}^{k}$.

Blackwell (1951), in his seminal work on comparison of experiments, ordered two experiments using a dilation ordering: one experiment, Y, is ‘more spread out’ in the sense of dilation than another one, X, if E(c(Y))≥E(c(X)) for all convex functions c. He showed that this ordering is equivalent to two other orderings, namely (i) a total time on test ordering and (ii) a martingale relationship E(Yʹ | Xʹ)=Xʹ, where (Xʹ,Yʹ) has a joint distribution with the same marginals as X and Y. These comparisons are generalized to balayage orderings that are defined in terms of generalized convex functions. These balayage orderings are equivalent to (i) iterated total integral of survival orderings and (ii) martingale-type orderings which we refer to as k-mart orderings. These comparisons can arise naturally in model fitting and data confidentiality contexts.

An RC-group is a unital group G with a distinguished compression base with respect to which G satisfies the Rickart projection and general comparison properties. We prove that a monotone $\sigma$-complete RC-group is a union of subgroups each of which is a lattice-ordered Dedekind $\sigma$-complete RC-group.

We obtain a new representation for the solution to the operator Sylvester equation in the form of a Stieltjes operator integral. We also formulate new sufficient conditions for the strong solvability of the operator Riccati equation that ensures the existence of reducing graph subspaces for block operator matrices. Next, we extend the concept of the Lifshits-Krein spectral shift function associated with a pair of self-adjoint operators to the case of pairs of admissible operators that are similar to self-adjoint operators. Based on this new concept we express the spectral shift function arising in a perturbation problem for block operator matrices in terms of the angular operators associated with the corresponding perturbed and unperturbed eigenspaces.

In this paper we formulate and solve Nevanlinna-Pick and Carathéodory type problems for tensor algebras with data given on the $N$-dimensional operator unit ball of a Hilbert space. We develop an approach based on the displacement structure theory.

Our objective in this sequel to $[18]$ is to develop extensions, to representations of tensor algebras over ${{C}^{*}}$-correspondences, of two fundamental facts about isometries on Hilbert space: The Wold decomposition theorem and Beurling’s theorem, and to apply these to the analysis of the invariant subspace structure of certain subalgebras of Cuntz-Krieger algebras.

An extension of the Naimark dilation theorem [N], [SzF2] to positive-definite functions on free semigroups is given. This is used to extend the operatorial trigonometric moment problem [A] to a non-commutative setting and to characterize the classes 𝐶ρ (ρ > 0) of all n-tuples of operators that have a p-isometric dilation (see [SzF2] for the case n = 1). It is also shown that 𝐶ρ ⊂ 𝐶ρ′ and 𝐶ρ ≠ 𝐶ρ′ for 0 < ρ < ρ′ < ∞.

The von Neumann inequality [vN], [Po2] is extended to the classes 𝐶p. This is used to prove that any element in 𝐶ρ is simultaneously similar to an element in 𝐶1.

For every m-tuple of operators acting on a Hilbert space, it is shown that there exists a common dilation of these operators to mcommuting normal operators on some larger Hilbert space. We then introduce a norm on the m-fold cartesian product of ℬ(ℋ) that is defined to be, for a given w-tuple, the infimum of the joint spectral radii of all joint normal dilations of the m operators. This norm has several good features, one of which is that it is invariant under the passage to adjoints.

We study a class of matrices (introduced by T. Kato) with principal homogeneous part, and use Mellin transform of the homogeneous kernel to determine spectral density of the positive infinite matrices.