Let $\Omega \subset \mathbb {R}^{n+1}$ , $n\ge 2$ , be a $1$ -sided nontangentially accessible domain, that is, a set which is quantitatively open and path-connected. Assume also that $\Omega $ satisfies the capacity density condition. Let $L_0 u=-\mathop {\operatorname {div}}\nolimits (A_0 \nabla u)$ , $Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$ be two real (not necessarily symmetric) uniformly elliptic operators in $\Omega $ , and write $\omega _{L_0}, \omega _L$ for the respective associated elliptic measures. We establish the equivalence between the following properties: (i) $\omega _L \in A_{\infty }(\omega _{L_0})$ , (ii) L is $L^p(\omega _{L_0})$ -solvable for some $p\in (1,\infty )$ , (iii) bounded null solutions of L satisfy Carleson measure estimates with respect to $\omega _{L_0}$ , (iv) $\mathcal {S}<\mathcal {N}$ (i.e., the conical square function is controlled by the nontangential maximal function) in $L^q(\omega _{L_0})$ for some (or for all) $q\in (0,\infty )$ for any null solution of L, and (v) L is $\mathrm {BMO}(\omega _{L_0})$ -solvable. Moreover, in each of the properties (ii)-(v) it is enough to consider the class of solutions given by characteristic functions of Borel sets (i.e, $u(X)=\omega _L^X(S)$ for an arbitrary Borel set $S\subset \partial \Omega $ ).

Also, we obtain a qualitative analog of the previous equivalences. Namely, we characterize the absolute continuity of $\omega _{L_0}$ with respect to $\omega _L$ in terms of some qualitative local $L^2(\omega _{L_0})$ estimates for the truncated conical square function for any bounded null solution of L. This is also equivalent to the finiteness $\omega _{L_0}$ -almost everywhere of the truncated conical square function for any bounded null solution of L. As applications, we show that $\omega _{L_0}$ is absolutely continuous with respect to $\omega _L$ if the disagreement of the coefficients satisfies some qualitative quadratic estimate in truncated cones for $\omega _{L_0}$ -almost everywhere vertex. Finally, when $L_0$ is either the transpose of L or its symmetric part, we obtain the corresponding absolute continuity upon assuming that the antisymmetric part of the coefficients has some controlled oscillation in truncated cones for $\omega _{L_0}$ -almost every vertex.

Adjacent dyadic systems are pivotal in analysis and related fields to study continuous objects via collections of dyadic ones. In our prior work (joint with Jiang, Olson, and Wei), we describe precise necessary and sufficient conditions for two dyadic systems on the real line to be adjacent. Here, we extend this work to all dimensions, which turns out to have many surprising difficulties due to the fact that $d+1$, not $2^d$, grids is the optimal number in an adjacent dyadic system in $\mathbb {R}^d$. As a byproduct, we show that a collection of $d+1$ dyadic systems in $\mathbb {R}^d$ is adjacent if and only if the projection of any two of them onto any coordinate axis are adjacent on $\mathbb {R}$. The underlying geometric structures that arise in this higher-dimensional generalization are interesting objects themselves, ripe for future study; these lead us to a compact, geometric description of our main result. We describe these structures, along with what adjacent dyadic (and n-adic, for any n) systems look like, from a variety of contexts, relating them to previous work, as well as illustrating a specific exa.

We present new estimates in the setting of weighted Lorentz spaces of operators satisfying a limited Rubio de Francia condition; namely $T$ is bounded on $L^{p}(v)$ for every $v$ in an strictly smaller class of weights than the Muckenhoupt class $A_p$. Important examples will be the Bochner–Riesz operators $BR_\lambda$ with $0<\lambda <{(n-1)}/2$, sparse operators, Hörmander multipliers with a limited regularity condition and rough operators with $\Omega \in L^{r}(\Sigma )$, $1 < r < \infty$.

Our first result is a noncommutative form of the Jessen-Marcinkiewicz-Zygmund theorem for the maximal limit of multiparametric martingales or ergodic means. It implies bilateral almost uniform convergence (a noncommutative analogue of almost everywhere convergence) with initial data in the expected Orlicz spaces. A key ingredient is the introduction of the $L_p$ -norm of the $\limsup $ of a sequence of operators as a localized version of a $\ell _\infty /c_0$ -valued $L_p$ -space. In particular, our main result gives a strong $L_1$ -estimate for the $\limsup $ —as opposed to the usual weak $L_{1,\infty }$ -estimate for the $\mathop {\mathrm {sup}}\limits $ —with interesting consequences for the free group algebra.

Let $\mathcal{L} \mathbf{F} _2$ denote the free group algebra with $2$ generators, and consider the free Poisson semigroup generated by the usual length function. It is an open problem to determine the largest class inside $L_1(\mathcal{L} \mathbf{F} _2)$ for which the free Poisson semigroup converges to the initial data. Currently, the best known result is $L \log ^2 L(\mathcal{L} \mathbf{F} _2)$ . We improve this result by adding to it the operators in $L_1(\mathcal{L} \mathbf{F} _2)$ spanned by words without signs changes. Contrary to other related results in the literature, this set grows exponentially with length. The proof relies on our estimates for the noncommutative $\limsup $ together with new transference techniques.

We also establish a noncommutative form of Córdoba/Feffermann/Guzmán inequality for the strong maximal: more precisely, a weak $(\Phi ,\Phi )$ inequality—as opposed to weak $(\Phi ,1)$ —for noncommutative multiparametric martingales and $\Phi (s) = s (1 + \log _+ s)^{2 + \varepsilon }$ . This logarithmic power is an $\varepsilon $ -perturbation of the expected optimal one. The proof combines a refinement of Cuculescu’s construction with a quantum probabilistic interpretation of M. de Guzmán’s original argument. The commutative form of our argument gives the simplest known proof of this classical inequality. A few interesting consequences are derived for Cuculescu’s projections.

We study the regularity of convolution powers for measures supported on Salem sets, and prove related results on Fourier restriction and Fourier multipliers. In particular we show that for $\alpha $ of the form $d\,/\,n,\,n\,=\,2,3,...$ there exist $\alpha $-Salem measures for which the ${{L}^{2}}$ Fourier restriction theorem holds in the range $p\,\le \,\frac{2d}{2d\,-\,\alpha }$. The results rely on ideas of Körner. We extend some of his constructions to obtain upper regular $\alpha $-Salem measures, with sharp regularity results for $n$-fold convolutions for all $n\,\in \,\mathbb{N}$.

In an extrapolation argument, we prove certain $L^{p}\,(1<p<\infty )$ estimates for nonisotropic Marcinkiewicz operators associated to surfaces under the integral kernels given by the elliptic sphere functions ${\rm\Omega}\in L(\log ^{+}L)^{{\it\alpha}}({\rm\Sigma})$ and the radial function $h\in {\mathcal{N}}_{{\it\beta}}(\mathbb{R}^{+})$. As applications, the corresponding results for parametric Marcinkiewicz integral operators related to area integrals and Littlewood–Paley $g_{{\it\lambda}}^{\ast }$-functions are given.

In this paper we characterize the compactness of the commutator $\left[ b,\,T \right]$ for the singular integral operator on the Morrey spaces 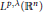${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$. More precisely, we prove that if 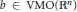$b\,\in \,\text{VMO}\left( {{\mathbb{R}}^{n}} \right)$, the 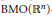$\text{BMO}\left( {{\mathbb{R}}^{n}} \right)$-closure of 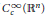$C_{c}^{\infty }\left( {{\mathbb{R}}^{n}} \right)$, then $\left[ b,\,T \right]$ is a compact operator on the Morrey spaces 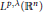${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ for 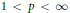$1\,<\,p\,<\,\infty $ and 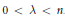$0\,<\,\lambda \,<\,n$. Conversely, if 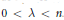$b\,\in \,\text{BMO}\left( {{\mathbb{R}}^{n}} \right)$ and $\left[ b,\,T \right]$ is a compact operator on the 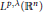${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ for some 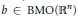$p\,\left( 1\,<\,p\,<\,\infty \right)$, then $b\,\in \,\text{VMO}\left( {{\mathbb{R}}^{n}} \right)$. Moreover, the boundedness of a rough singular integral operator 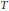$T$ and its commutator $\left[ b,\,T \right]$ on 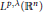${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ are also given. We obtain a sufficient condition for a subset in Morrey space to be a strongly pre-compact set, which has interest in its own right.

A class of generalized Marcinkiewicz integral operators is introduced, and, under rather weak conditions on the integral kernels, the boundedness of such operators on ${{L}^{p}}$ and Triebel–Lizorkin spaces is established.

Weconsider the Fourier restriction operators associated to certaindegenerate curves in ℝd for which the highest torsion vanishes. We prove estimates with respect to affine arclength and with respect to the Euclidean arclength measure on the curve. The estimates have certain uniform features, and the affine arclength results cover families of flat curves.

In this paper, a proof is given that certain boundedness properties of operators yield distributional estimates that have exponential decay at infinity. Such distributional estimates imply local exponential integrability, and apply to many operators such as $m$-linear Calderón–Zygmund operators and their maximal counterparts.

In this note the authors give the L2(n) boundedness of a class of parametric Marcinkiewicz integral with kernel function Ω in L log+L(Sn−1) and radial function h(|x|) ∈ l ∞ l(Lq)(+) for 1 < q ≦.

As its corollary, the Lp (n)(2 < p < ∞) boundedness of and and with Ω in L log+L (Sn-1) and h(|x|) ∈ l∞ (Lq)(+) are also obtained. Here and are parametric Marcinkiewicz functions corresponding to the Littlewood-Paley g*λ-function and the Lusin area function S, respectively.

We prove that the ${{L}^{2}}$ restriction theorem, and ${{L}^{p}}\,\to \,{{L}^{{{p}'}}}\,,\,\frac{1}{p}\,+\,\frac{1}{{{p}'}}\,=\,1$, boundedness of the surface averages imply certain geometric restrictions on the underlying hypersurface. We deduce that these bounds imply that a certain number of principal curvatures do not vanish.

We consider a convolution singular integral operator associated to a kernel K(x) = b(x)Ω(x)|x|-n, and prove that if b ∊ L∞(ℝn) is a radial function and Ω ∊ H(Σn-1) with mean zero condition (1), then is a bounded linear operator in the space L2(ℝn).

Suppose that a subset of a finite dimensional lattice has the property that there are many orthogonal tensor products that are almost 1 on the set, then the set is forced to have unusual concentrations of points in small cartesian products.