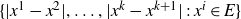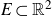In this paper we prove that the set $\{|x^1-x^2|,\dots,|x^k-x^{k+1}|\,{:}\,x^i\in E\}$ has non-empty interior in $\mathbb{R}^k$ when $E\subset \mathbb{R}^2$ is a Cartesian product of thick Cantor sets 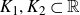$K_1,K_2\subset\mathbb{R}$. We also prove more general results where the distance map 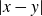$|x-y|$ is replaced by a function 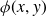$\phi(x,y)$ satisfying mild assumptions on its partial derivatives. In the process, we establish a nonlinear version of the classic Newhouse Gap Lemma, and show that if 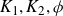$K_1,K_2, \phi$ are as above then there exists an open set S so that $\bigcap_{x \in S} \phi(x,K_1\times K_2)$ has non-empty interior.

In this paper, we consider the behavior of the commutators of convolution operators on the Triebel–Lizorkin spaces ${{\dot{F}}_{p}}^{s,q}$.

Wiener-Lorentz amalgam spaces are introduced and some of their interpolation theoretic properties are discussed. We prove Hausdorff-Young theorems for these spaces unifying and extending Hunt's Hausdorff-Young theorem for Lorentz spaces and Holland's theorem for amalgam spaces. As consequences we prove weighted norm inequalities for the Fourier transform and show how these inequalities fit into a natural class of weighted Fourier transform estimates