We show that if  $m,n\ge 0,\lambda >1$, and
$m,n\ge 0,\lambda >1$, and 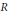 $R$ is a rational function with numerator, denominator of degree
$R$ is a rational function with numerator, denominator of degree 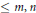 $\le m,n$, respectively, then there exists a set
$\le m,n$, respectively, then there exists a set 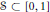 $S\subset [0,1]$ of linear measure
$S\subset [0,1]$ of linear measure 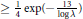 $\ge \,\frac{1}{4}\,\exp \left( -\frac{13}{\log \,\text{ }\!\!\lambda\!\!\text{ }} \right)$ such that for
$\ge \,\frac{1}{4}\,\exp \left( -\frac{13}{\log \,\text{ }\!\!\lambda\!\!\text{ }} \right)$ such that for 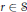 $r\in S$,
$r\in S$,
1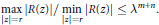 $$_{|z|=r\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,|z|=r}^{\max |R(z)|/min|R(z)|\le {{\lambda }^{m+n}}.}$$
$$_{|z|=r\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,|z|=r}^{\max |R(z)|/min|R(z)|\le {{\lambda }^{m+n}}.}$$
Here, one may not replace 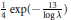 $\frac{1}{4}\exp (-\frac{13}{\log \lambda })$ by
$\frac{1}{4}\exp (-\frac{13}{\log \lambda })$ by  $\exp (-\frac{2-\varepsilon }{\log \lambda })$, for any
$\exp (-\frac{2-\varepsilon }{\log \lambda })$, for any 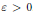 $\varepsilon >0$. As our motivating application, we prove a convergence result for diagonal Padé approximants for functions meromorphic in the unit ball.
$\varepsilon >0$. As our motivating application, we prove a convergence result for diagonal Padé approximants for functions meromorphic in the unit ball.