In this paper we give the form of every multiplicative Hausdorff prime matrix, thus answering a long-standing open question.

Let $A={{({{a}_{j,k}})}_{j,k\ge 1}}$ be a non-negative matrix. In this paper, we characterize those $A$ for which ${{\left\| A \right\|}_{E,F}}$ are determined by their actions on decreasing sequences, where $E$ and $F$ are suitable normed Riesz spaces of sequences. In particular, our results can apply to the following spaces: ${{\ell }_{p}}$, $d(w,p)$, and ${{\ell }_{p}}(w)$. The results established here generalize ones given by Bennett; Chen, Luor, and Ou; Jameson; and Jameson and Lashkaripour.

We consider Hausdorff and quasi-Hausdorff matrices as operators on classical spaces of analytic functions such as the Hardy and the Bergman spaces, the Dirichlet space, the Bloch spaces and $\text{BMOA}$. When the generating sequence of the matrix is the moment sequence of a measure $\mu$, we find the conditions on $\mu$ which are equivalent to the boundedness of the matrix on the various spaces.

Abstract. The weighted mean matrix 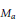${{M}_{a}}$ is the triangular matrix 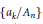$\left\{ {{a}_{k}}/{{A}_{n}} \right\}$, where 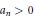${{a}_{n}}\,>\,0$ and 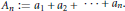${{A}_{n}}\,:=\,{{a}_{1}}\,+\,{{a}_{2}}\,+\cdots +\,{{a}_{n}}$. It is proved that, subject to 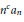${{n}^{c}}{{a}_{n}}$ being eventually monotonic for each constant 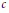$c$ and to the existence of 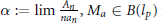$\alpha \,:=\,\lim \,\frac{{{A}_{n}}}{n{{a}_{n}}},\,{{M}_{a}}\,\in \,B\left( {{l}_{p}} \right)$ for 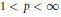$1\,<\,p\,<\infty $ if and only if 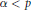$\alpha \,<\,p$.

The two theorems proved yield simple yet reasonably general conditions for triangular matrices to be bounded operators on ${{l}_{p}}$. The theorems are applied to Nörlund and weighted mean matrices.

The Nörlund matrix Na is the triangular matrix {an-k /An}, where an ≥ 0 and An := a0 + a1 + • • • + an > 0. It is proved that, subject to the existence of α := lim nan/An, Na ∊ B(lp) for 1 < p < ∞ if and only if α < ∞. It is also proved that it is possible to have Na ∊ B(lp) for 1 < p < ∞ when sup nan/An = ∞.

Our main result is a Tauberian theorem for the general Euler-Borel summability method. Examples of the method include the discrete Borel, Euler, Meyer- Kônig, Taylor and Karamata methods. Every function/ analytic on the closed unit disk and satisfying some general conditions generates such a method, denoted by (£,ƒ). For instance the function ƒ(z) = exp(z — 1) generates the discrete Borel method. To each such function ƒ corresponds an even positive integer p = p(f).We show that if a sequence (sn)is summable (E,f)and as n→ ∞ m > n, (m— n)n-p(f)→0, then (sn)is convergent. If the Maclaurin coefficients of/ are nonnegative, then p(f) =2. In this case we may replace the condition . This generalizes the Tauberian theorems for Borel summability due to Hardy and Littlewood, and R. Schmidt. We have also found new examples of the method and proved that the exponent —p(f)in the Tauberian condition (*) is the best possible.

In this paper we obtain the bv0-norms for several well-known classes of matrix operators.

Our main result is the following monotonicity property for moment sequences μ. Let p be fixed, 1 ≤ p < ∞: then

is an increasing function of r(r = 1,2,…). From this we derive a sharp lower bound for an arbitrary Hausdorff matrix acting on ℓp.The corresponding upper bound problem was solved by Hardy.

In a recent paper D. Borwein [Math. Z. 183(1983), 483- 487] obtained an upper bound for the lp -norms of some generalized Hausdorff matrices, where the sequence (λn) satisfies the condition λn+1 ≦ λn + c, for some positive c. In this paper we obtained the lp -norms of these generalized Hausdorff matrices for which the mass functions are totally monotone.

Nӧrlund methods of summability are studied as mappings from I1 into I1. Conditions are given for an arbitrary l-l method to include a Nӧrlund method. In particular necessary and sufficient conditions are given for a row finite l-l method to include a Nӧrlund mean.