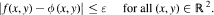We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We determine the general solutions of the functional equation 
for ƒi: G → F (i = 1,2,3,4), where G is a 2-divisible group and F is a commutative field of characteristic different from 2. The motivation for studying this equation came from a result due to Dry gas [4] where he proved a Jordan and von Neumann type characterization theorem for quasi-inner products. Also, this equation is a generalization of the quadratic functional equation investigated by several authors in connection with inner product spaces and their generalizations. Special cases of this equation include the Cauchy equation, the Jensen equation, the Pexider equation and many more. Here, we determine the general solution of this equation without any regularity assumptions on ƒi.
For h € ℝ and ϕ : ℝ2 → ℝ define Lhϕ: ℝ2 → ℝ by (Lhϕ)(x, y) = ϕ (x + h, y) + ϕ (x — h,y) — ϕ (x,y + h) — ϕ (x,y — h) for all (x,y) € ℝ2. The aim of the paper is to establish the following "stability" theorem concerning the functional equation
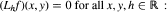
if δ > 0, f : ℝ2 → ℝ and
then there exists ɛ > 0 ami ϕ : ℝ2 → ℝ such that (Lhϕ)(x, y ) = 0 for all x, y,h ∊ ℝ and
