For $s_1,\,s_2\in (0,\,1)$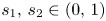 and $p,\,q \in (1,\, \infty )$
and $p,\,q \in (1,\, \infty )$ , we study the following nonlinear Dirichlet eigenvalue problem with parameters $\alpha,\, \beta \in \mathbb {R}$
, we study the following nonlinear Dirichlet eigenvalue problem with parameters $\alpha,\, \beta \in \mathbb {R}$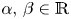 driven by the sum of two nonlocal operators:
driven by the sum of two nonlocal operators:\[ (-\Delta)^{s_1}_p u+(-\Delta)^{s_2}_q u=\alpha|u|^{p-2}u+\beta|u|^{q-2}u\ \text{in }\Omega, \quad u=0\ \text{in } \mathbb{R}^d \setminus \Omega, \quad \mathrm{(P)} \]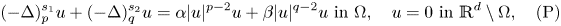
where $\Omega \subset \mathbb {R}^d$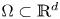 is a bounded open set. Depending on the values of $\alpha,\,\beta$
is a bounded open set. Depending on the values of $\alpha,\,\beta$ , we completely describe the existence and non-existence of positive solutions to (P). We construct a continuous threshold curve in the two-dimensional $(\alpha,\, \beta )$
, we completely describe the existence and non-existence of positive solutions to (P). We construct a continuous threshold curve in the two-dimensional $(\alpha,\, \beta )$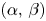 -plane, which separates the regions of the existence and non-existence of positive solutions. In addition, we prove that the first Dirichlet eigenfunctions of the fractional $p$
-plane, which separates the regions of the existence and non-existence of positive solutions. In addition, we prove that the first Dirichlet eigenfunctions of the fractional $p$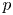 -Laplace and fractional $q$
-Laplace and fractional $q$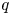 -Laplace operators are linearly independent, which plays an essential role in the formation of the curve. Furthermore, we establish that every nonnegative solution of (P) is globally bounded.
-Laplace operators are linearly independent, which plays an essential role in the formation of the curve. Furthermore, we establish that every nonnegative solution of (P) is globally bounded.