We first prove that the realization $A_{\mathrm {min}}$ of $A:={\operatorname {\mathrm {div}}}(Q\nabla )-V$ in $L^2({\mathbb {R}}^d)$ with unbounded coefficients generates a symmetric sub-Markovian and ultracontractive semigroup on $L^2({\mathbb {R}}^d)$ which coincides on $L^2({\mathbb {R}}^d)\cap C_b({\mathbb {R}}^d)$ with the minimal semigroup generated by a realization of $A$ on $C_b({\mathbb {R}}^d)$. Moreover, using time-dependent Lyapunov functions, we prove pointwise upper bounds for the heat kernel of $A$ and deduce some spectral properties of $A_{\min }$ in the case of polynomially and exponentially growing diffusion and potential coefficients.

In this paper we consider uncertainty principles for solutions of certain partial differential equations on $H$-type groups. We first prove that, on $H$-type groups, the heat kernel is an average of Gaussians in the central variable, so that it does not satisfy a certain reformulation of Hardy’s uncertainty principle. We then prove the analogue of Hardy’s uncertainty principle for solutions of the Schrödinger equation with potential on $H$-type groups. This extends the free case considered by Ben Saïd et al. [‘Uniqueness of solutions to Schrödinger equations on H-type groups’, J. Aust. Math. Soc. (3)95 (2013), 297–314] and by Ludwig and Müller [‘Uniqueness of solutions to Schrödinger equations on 2-step nilpotent Lie groups’, Proc. Amer. Math. Soc.142 (2014), 2101–2118].

Let $X$ be a space of homogeneous type and $L$ be a nonnegative self-adjoint operator on $L^{2}(X)$ satisfying Gaussian upper bounds on its heat kernels. In this paper, we develop the theory of weighted Besov spaces ${\dot{B}}_{p,q,w}^{\unicode[STIX]{x1D6FC},L}(X)$ and weighted Triebel–Lizorkin spaces ${\dot{F}}_{p,q,w}^{\unicode[STIX]{x1D6FC},L}(X)$ associated with the operator $L$ for the full range $0<p,q\leqslant \infty$, $\unicode[STIX]{x1D6FC}\in \mathbb{R}$ and $w$ being in the Muckenhoupt weight class $A_{\infty }$. Under rather weak assumptions on $L$ as stated above, we prove that our new spaces satisfy important features such as continuous characterizations in terms of square functions, atomic decompositions and the identifications with some well-known function spaces such as Hardy-type spaces and Sobolev-type spaces. One of the highlights of our result is the characterization of these spaces via noncompactly supported functional calculus. An important by-product of this characterization is the characterization via the heat kernel for the full range of indices. Moreover, with extra assumptions on the operator $L$, we prove that the new function spaces associated with 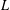$L$ coincide with the classical function spaces. Finally we apply our results to prove the boundedness of the fractional power of $L$, the spectral multiplier of 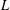$L$ in our new function spaces and the dispersive estimates of wave equations.

We consider a second-order elliptic operator L in skew product of an ordinary differential operator L1 on an interval (a, b) and an elliptic operator on a domain D2 of a Riemannian manifold such that the associated heat kernel is intrinsically ultracontractive. We give criteria for criticality and subcriticality of L in terms of a positive solution having minimal growth at η (η = a, b) to an associated ordinary differential equation. In the subcritical case, we explicitly determine the Martin compactification and Martin kernel for L on the basis of [24]; in particular, the Martin boundary over η is either one point or a compactification of D2, which depends on whether an associated integral near η diverges or converges. From this structure theorem we show a monotonicity property that the Martin boundary over η does not become smaller as the potential term of L1 becomes larger near η.

In this paper we prove a short time asymptotic expansion of a hypoelliptic heat kernel on a Euclidean space and a compact manifold. We study the ‘cut locus’ case, namely, the case where energy-minimizing paths which join the two points under consideration form not a finite set, but a compact manifold. Under mild assumptions we obtain an asymptotic expansion of the heat kernel up to any order. Our approach is probabilistic and the heat kernel is regarded as the density of the law of a hypoelliptic diffusion process, which is realized as a unique solution of the corresponding stochastic differential equation. Our main tools are S. Watanabe’s distributional Malliavin calculus and T. Lyons’ rough path theory.

Let $(X,d,{\it\mu})$ be a metric measure space satisfying the doubling, reverse doubling and noncollapsing conditions. Let $\mathscr{L}$ be a nonnegative self-adjoint operator on $L^{2}(X,d{\it\mu})$ satisfying a pointwise Gaussian upper bound estimate and Hölder continuity for its heat kernel. In this paper, we introduce the Hardy spaces $H_{\mathscr{L}}^{p}(X)$, $0<p\leq 1$, associated to $\mathscr{L}$ in terms of grand maximal functions and show that these spaces are equivalently characterised by radial and nontangential maximal functions.

We prove that, in a setting of local Dirichlet forms on metric measure spaces, a two-sided sub-Gaussian estimate of the heat kernel is equivalent to the conjunction of the volume doubling property, the elliptic Harnack inequality, and a certain estimate of the capacity between concentric balls. The main technical tool is the equivalence between the capacity estimate and the estimate of a mean exit time in a ball that uses two-sided estimates of a Green function in a ball.