Let y be the solution of the equation
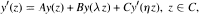
where A, B, C, λ and η aie complex numbers and  It is shown that y has exponential order equal to one if A ≠ 0 and if y is not a polynomial; otherwise, y has exponential order equal to zero. In the latter case, y and all of its derivatives are unbounded on any ray.
It is shown that y has exponential order equal to one if A ≠ 0 and if y is not a polynomial; otherwise, y has exponential order equal to zero. In the latter case, y and all of its derivatives are unbounded on any ray.