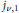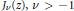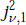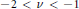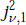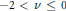Let ${{j}_{v,1}}$ be the smallest (first) positive zero of the Bessel function ${{J}_{v}}(z),\,v\,>\,-\,1$, which becomes zero when $v$ approaches −1. Then $j_{v,1}^{2}$ can be continued analytically to $-2\,<\,v\,<\,-1$, where it takes on negative values. We show that $j_{v,1}^{2}$ is a convex function of $v$ in the interval $-2\,<\,v\,\le \,0$, as an addition to an old result [Á. Elbert and A. Laforgia, SIAM J. Math. Anal. 15(1984), 206–212], stating this convexity for 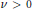$v\,>\,0$. Also the monotonicity properties of the functions $\frac{j_{v,1}^{2}}{4(v+1)},\,\frac{j_{v,1}^{2}}{4(v+1)\sqrt{v+2}}$ are determined. Our approach is based on the series expansion of Bessel function ${{J}_{v}}(z)$ and it turned out to be effective, especially when 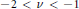$-2\,<\,v\,<\,-1$.

Convergence results are given for transient characteristics of an M/M/∞ system such as the period of time the occupation process remains above a given state, the area swept by this process above this state and the number of customers arriving during this period. These results are precise in contrast to approximations derived in the framework of the Poisson clumping heuristic introduced by Aldous.

We show, among other things, that, for n = 0,1, the negative of the square of a purely imaginary zero of is unimodal on (n — 2, n — 1). One of the important tools in the proof is the Mittag-Leffler partial fractions expansion of .

We study a class of generalized hypergeometric functions in several variables introduced by A. Korânyi. It is shown that the generalized Gaussian hypergeometric function is the unique solution of a system partial differential equations. Analogues of some classical results such as Kummer relations and Euler integral representations are established. Asymptotic behavior of generalized hypergeometric functions is obtained which includes some known estimates.

We consider the positive zeros j″vk, k = 1, 2,…, of the second derivative of the Bessel function Jν(x). We are interested first in how many zeros there are on the interval (0,jν1), where jν1 is the smallest positive zero of Jν(x). We show that there exists a number ƛ = —0.19937078… such that and . Moreover, j″v1 decreases to 0 and j″ν2 increases to j″01 as ν increases from ƛ to 0. Further, j″vk increases in —1 < ν< ∞, for k = 3,4,… Monotonicity properties are established also for ordinates, and the slopes at the ordinates, of the points of inflection when — 1 < ν < 0.

Let jν, 1, jν,2, … denote the positive zeros of the Bessel function Jν(x), and similarly, let j'v,1, j'v,2, … denote the positive zeros of J'v(x), which are the positive critical points of Jv(x). It is well-known that when v is positive, both jν ,k. it and j'ν k are increasing functions of ν; see, e.g., [12, pp. 246 and 248]. Recently, Lorch and Szego [6] have attempted to show that the same is true for the positive zeros j″v,1, j″v,2, … of j″v(x), which are the positive inflection points of Jv(x).

The solutions of a certain class of first order linear differential equations are shown to be either completely or absolutely monotone depending on the nature of its coefficients. This is a simple theorem which is used to deduce a number of new and interesting results dealing with the complete and absolute monotonicity of functions. In particular, a partial answer is supplied to a question posed by Askey and Pollard: “When is completely monotone?”