We shall explain here an idea to generalize classical complex analytic Kleinian group theory to any odd-dimensional cases. For a certain class of discrete subgroups of $\text{PGL}_{2n+1}(\mathbf{C})$ acting on $\mathbf{P}^{2n+1}$, we can define their domains of discontinuity in a canonical manner, regarding an $n$-dimensional projective linear subspace in $\mathbf{P}^{2n+1}$ as a point, like a point in the classical one-dimensional case. Many interesting (compact) non-Kähler manifolds appear systematically as the canonical quotients of the domains. In the last section, we shall give some examples.

We prove the vanishing and non-vanishing theorems for an intersection of a finite number of q-complete domains in a complex manifold of dimension n. When q does not divide n, it is stronger than the result naturally obtained by combining the approximation theorem of Diederich-Fornaess for q-convex functions with corners and the vanishing theorem of Andreotti-Grauert for q-complete domains. We also give an example which implies our result is best possible.

We study the existence of L2 holomorphic sections of invariant line bundles over Galois coverings. We show that the von Neumann dimension of the space of L2 holomorphic sections is bounded below under weak curvature conditions. We also give criteria for a compact complex space with isolated singularities and some related strongly pseudoconcave manifolds to be Moishezon. As applications we prove the stability of the previous Moishezon pseudoconcave manifolds under perturbation of complex structures as well as weak Lefschetz theorems.

We develop some symplectic techniques to control the behavior under symplectic transformation of analytic discs A of X = ℂn tangent to a real generic submanifold R and contained in a wedge with edge R.

We show that if A* is a lift of A to T* X and if χ is a symplectic transformation between neighborhoods of po and qo, then A is orthogonal to po if and only if Ã:= πχA* is orthogonal to qo. Also we give the (real) canonical form of the couples of hypersurfaces of ℝ2n ⋍ ℂn whose conormal bundles have clean intersection. This generalizes [10] to general dimension of intersection.

Combining this result with the quantized action on sheaves of the “tuboidal” symplectic transformation, we show the following: If R, S are submanifolds of X with R ⊂ S and 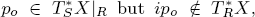then the conditions 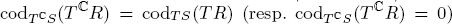can be characterized as opposite inclusions for the couple of closed half-spaces with conormal bundles

In §3 we give some partial applications of the above result to the analytic hypoellipticity of CR hyperfunctions on higher codimensional manifolds by the aid of discs (cf. [2], [3] as for the case of hypersurfaces).