Let $T = (T_1, \ldots , T_n)$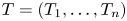 be a commuting tuple of bounded linear operators on a Hilbert space $\mathcal{H}$
be a commuting tuple of bounded linear operators on a Hilbert space $\mathcal{H}$ . The multiplicity of $T$
. The multiplicity of $T$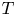 is the cardinality of a minimal generating set with respect to $T$
is the cardinality of a minimal generating set with respect to $T$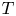 . In this paper, we establish an additive formula for multiplicities of a class of commuting tuples of operators. A special case of the main result states the following: Let $n \geq 2$
. In this paper, we establish an additive formula for multiplicities of a class of commuting tuples of operators. A special case of the main result states the following: Let $n \geq 2$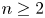 , and let $\mathcal{Q}_i$
, and let $\mathcal{Q}_i$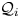 , $i = 1, \ldots , n$
, $i = 1, \ldots , n$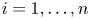 , be a proper closed shift co-invariant subspaces of the Dirichlet space or the Hardy space over the unit disc in $\mathbb {C}$
, be a proper closed shift co-invariant subspaces of the Dirichlet space or the Hardy space over the unit disc in $\mathbb {C}$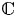 . If $\mathcal{Q}_i^{\bot }$
. If $\mathcal{Q}_i^{\bot }$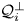 , $i = 1, \ldots , n$
, $i = 1, \ldots , n$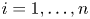 , is a zero-based shift invariant subspace, then the multiplicity of the joint $M_{\textbf {z}} = (M_{z_1}, \ldots , M_{z_n})$
, is a zero-based shift invariant subspace, then the multiplicity of the joint $M_{\textbf {z}} = (M_{z_1}, \ldots , M_{z_n})$ -invariant subspace $(\mathcal{Q}_1 \otimes \cdots \otimes \mathcal{Q}_n)^{\perp }$
-invariant subspace $(\mathcal{Q}_1 \otimes \cdots \otimes \mathcal{Q}_n)^{\perp }$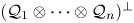 of the Dirichlet space or the Hardy space over the unit polydisc in $\mathbb {C}^{n}$
of the Dirichlet space or the Hardy space over the unit polydisc in $\mathbb {C}^{n}$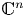 is given by
is given by
\[ \mbox{mult}_{M_{\textbf{{z}}}|_{ (\mathcal{Q}_1 \otimes \cdots \otimes \mathcal{Q}_n)^{{\perp}}}} (\mathcal{Q}_1 \otimes \cdots \otimes \mathcal{Q}_n)^{{\perp}} = \sum_{i=1}^{n} (\mbox{mult}_{M_z|_{\mathcal{Q}_i^{{\perp}}}} (\mathcal{Q}_i^{\bot})) = n. \]
A similar result holds for the Bergman space over the unit polydisc.
 $\mathcal{M}$-Harmonic Conjugate Operator
$\mathcal{M}$-Harmonic Conjugate Operator