We study the symplectic leaves of the subvariety of fixed points of an automorphism of a Calogero–Moser space induced by an element of finite order of the normalizer of the associated complex reflection group. We give a parametrization à la Harish-Chandra of its symplectic leaves (generalizing earlier works of Bellamy and Losev). This result is inspired by the mysterious relations between the geometry of Calogero–Moser spaces and unipotent representations of finite reductive groups, which is the theme of another paper, C. Bonnafé [‘Calogero–Moser spaces vs unipotent representations’, Pure Appl. Math. Q., to appear, Preprint, 2021, arXiv:2112.13684].

We compare crystal combinatorics of the level $2$ Fock space with the classification of unitary irreducible representations of type B rational Cherednik algebras to study how unitarity behaves under parabolic restriction. We show that the crystal operators that remove boxes preserve the combinatorial conditions for unitarity, and that the parabolic restriction functors categorifying the crystals send irreducible unitary representations to unitary representations. Furthermore, we find the supports of the unitary representations.

We will develop a theory of multi-pointed non-commutative deformations of a simple collection in an abelian category, and construct relative exceptional objects and relative spherical objects in some cases. This is inspired by a work by Donovan and Wemyss.

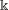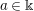Let $\Bbbk$ be a field of characteristic zero. For any positive integer $n$ and any scalar $a\in \Bbbk$, we construct a family of Artin–Schelter regular algebras $R(n,a)$, which are quantizations of Poisson structures on 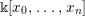$\Bbbk [x_{0},\ldots ,x_{n}]$. This generalizes an example given by Pym when 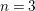$n=3$. For a particular choice of the parameter $a$ we obtain new examples of Calabi–Yau algebras when 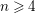$n\geqslant 4$. We also study the ring theoretic properties of the algebras 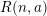$R(n,a)$. We show that the point modules of 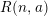$R(n,a)$ are parameterized by a bouquet of rational normal curves in 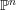$\mathbb{P}^{n}$, and that the prime spectrum of 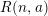$R(n,a)$ is homeomorphic to the Poisson spectrum of its semiclassical limit. Moreover, we explicitly describe 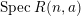$\operatorname{Spec}R(n,a)$ as a union of commutative strata.

Let ${\rm\Gamma}$ be a finite subgroup of $\text{Sp}(V)$. In this article we count the number of symplectic resolutions admitted by the quotient singularity $V/{\rm\Gamma}$. Our approach is to compare the universal Poisson deformation of the symplectic quotient singularity with the deformation given by the Calogero–Moser space. In this way, we give a simple formula for the number of $\mathbb{Q}$-factorial terminalizations admitted by the symplectic quotient singularity in terms of the dimension of a certain Orlik–Solomon algebra naturally associated to the Calogero–Moser deformation. This dimension is explicitly calculated for all groups ${\rm\Gamma}$ for which it is known that $V/{\rm\Gamma}$ admits a symplectic resolution. As a consequence of our results, we confirm a conjecture of Ginzburg and Kaledin.

We consider finite groups acting on quantum (or skew) polynomial rings. Deformations of the semidirect product of the quantum polynomial ring with the acting group extend symplectic reflection algebras and graded Hecke algebras to the quantum setting over a field of arbitrary characteristic. We give necessary and sufficient conditions for such algebras to satisfy a Poincaré–Birkhoff–Witt property using the theory of noncommutative Gröbner bases. We include applications to the case of abelian groups and the case of groups acting on coordinate rings of quantum planes. In addition, we classify graded automorphisms of the coordinate ring of quantum 3-space. In characteristic zero, Hochschild cohomology gives an elegant description of the Poincaré–Birkhoff–Witt conditions.

For a derivation δ of a commutative Noetherian ${\mathbb C}$-algebra A, a homeomorphism is established between the prime spectrum of the Ore extension A[z;δ] and the Poisson prime spectrum of the polynomial algebra A[z] endowed with the Poisson bracket such that {A,A}=0 and {z,a}=δ(a) for all a ∈ A.

We construct an interesting family of connected graded domains of Gel’fand–Kirillov dimension 4, and show that the general member of this family is noetherian. The algebras we construct are Koszul and have global dimension 4. They fail to be Artin–Schelter Gorenstein, however, showing that a theorem of Zhang and Stephenson for dimension 3 algebras does not extend to dimension 4. The Auslander–Buchsbaum formula also fails to hold for these algebras. The algebras we construct are birational to ℙ2, and their existence disproves a conjecture of the first author and Stafford. The algebras can be obtained as global sections of a certain quasicoherent graded sheaf on ℙ1×ℙ1, and our key technique is to work with this sheaf. In contrast to all previously known examples of birationally commutative graded domains, the graded pieces of the sheaf fail to be ample in the sense of Van den Bergh. Our results thus require significantly new techniques.

The defining relations for the Lie superalgebra Γ (σ1, σ2, σ3) as a contragredient algebra are discussed and a PBW type basis theorem is proved for the corresponding q-deformation.