Let  $R$ be a semiprime ring with center
$R$ be a semiprime ring with center 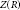 $Z\left( R \right)$. For
$Z\left( R \right)$. For 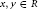 $x,\,y\,\in \,R$, we denote by
$x,\,y\,\in \,R$, we denote by 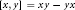 $\left[ x,\,y \right]\,=\,xy\,-\,yx$ the commutator of
$\left[ x,\,y \right]\,=\,xy\,-\,yx$ the commutator of  $x$ and
$x$ and  $y$. If
$y$. If  $\sigma $ is a non-identity automorphism of
$\sigma $ is a non-identity automorphism of  $R$ such that
$R$ such that
1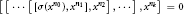 $$\left[ \left[ \cdot \cdot \cdot \,\left[ \left[ \sigma \left( {{x}^{n0}} \right),\,{{x}^{n1}} \right],\,{{x}^{n2}} \right],\cdot \cdot \cdot \right],\,{{x}^{nk}} \right]\,=\,0$$
$$\left[ \left[ \cdot \cdot \cdot \,\left[ \left[ \sigma \left( {{x}^{n0}} \right),\,{{x}^{n1}} \right],\,{{x}^{n2}} \right],\cdot \cdot \cdot \right],\,{{x}^{nk}} \right]\,=\,0$$
for all  $x\,\in \,R$, where
$x\,\in \,R$, where 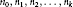 ${{n}_{0}},\,{{n}_{1}},\,{{n}_{2}},\,...,\,{{n}_{k}}$ are fixed positive integers, then there exists a map
${{n}_{0}},\,{{n}_{1}},\,{{n}_{2}},\,...,\,{{n}_{k}}$ are fixed positive integers, then there exists a map  $\mu \,:\,R\,\to \,Z\left( R \right)$ such that
$\mu \,:\,R\,\to \,Z\left( R \right)$ such that  $\sigma \left( x \right)\,=\,x\,+\,\mu \left( x \right)$ for all
$\sigma \left( x \right)\,=\,x\,+\,\mu \left( x \right)$ for all  $x\,\in \,R$. In particular, when
$x\,\in \,R$. In particular, when  $R$ is a prime ring,
$R$ is a prime ring,  $R$ is commutative.
$R$ is commutative.