We study the problem of determining, for a polynomial function  $f$ on a vector space
$f$ on a vector space 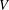 $V$, the linear transformations
$V$, the linear transformations 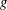 $g$ of
$g$ of  $V$ such that
$V$ such that 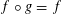 $f\circ g=f$. When
$f\circ g=f$. When 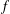 $f$ is invariant under a simple algebraic group
$f$ is invariant under a simple algebraic group 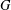 $G$ acting irreducibly on
$G$ acting irreducibly on 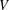 $V$, we note that the subgroup of
$V$, we note that the subgroup of 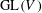 $\text{GL}(V)$ stabilizing
$\text{GL}(V)$ stabilizing 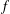 $f$ often has identity component
$f$ often has identity component 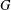 $G$, and we give applications realizing various groups, including the largest exceptional group
$G$, and we give applications realizing various groups, including the largest exceptional group 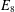 $E_{8}$, as automorphism groups of polynomials and algebras. We show that, starting with a simple group
$E_{8}$, as automorphism groups of polynomials and algebras. We show that, starting with a simple group 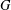 $G$ and an irreducible representation
$G$ and an irreducible representation 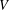 $V$, one can almost always find an
$V$, one can almost always find an 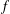 $f$ whose stabilizer has identity component
$f$ whose stabilizer has identity component 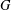 $G$, and that no such
$G$, and that no such 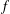 $f$ exists in the short list of excluded cases. This relies on our core technical result, the enumeration of inclusions
$f$ exists in the short list of excluded cases. This relies on our core technical result, the enumeration of inclusions  $G<H\leqslant \text{SL}(V)$ such that
$G<H\leqslant \text{SL}(V)$ such that 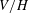 $V/H$ has the same dimension as
$V/H$ has the same dimension as  $V/G$. The main results of this paper are new even in the special case where
$V/G$. The main results of this paper are new even in the special case where 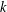 $k$ is the complex numbers.
$k$ is the complex numbers.