Let 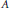 $A$ and
$A$ and  $B$ be
$B$ be 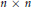 $n\,\times \,n$ complex Hermitian (or real symmetric) matrices with eigenvalues
$n\,\times \,n$ complex Hermitian (or real symmetric) matrices with eigenvalues 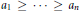 ${{a}_{1}}\,\ge \,\cdots \,\ge \,{{a}_{n}}$ and
${{a}_{1}}\,\ge \,\cdots \,\ge \,{{a}_{n}}$ and 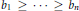 ${{b}_{1}}\,\ge \,\cdots \,\ge \,{{b}_{n}}$. All possible inertia values, ranks, and multiple eigenvalues of
${{b}_{1}}\,\ge \,\cdots \,\ge \,{{b}_{n}}$. All possible inertia values, ranks, and multiple eigenvalues of  $A\,+\,B$ are determined. Extension of the results to the sum of
$A\,+\,B$ are determined. Extension of the results to the sum of  $k$ matrices with
$k$ matrices with  $k\,>\,2$ and connections of the results to other subjects such as algebraic combinatorics are also discussed.
$k\,>\,2$ and connections of the results to other subjects such as algebraic combinatorics are also discussed.