We prove that if  $y''=f(y,y',t,\alpha ,\beta ,\ldots)$ is a generic Painlevé equation from among the classes II, IV and V, and if
$y''=f(y,y',t,\alpha ,\beta ,\ldots)$ is a generic Painlevé equation from among the classes II, IV and V, and if 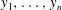 $y_1,\ldots,y_n$ are distinct solutions, then
$y_1,\ldots,y_n$ are distinct solutions, then 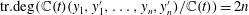 $\mathrm{tr.deg}(\mathbb{C}(t)(y_1,y'_1,\ldots,y_n,y'_n)/\mathbb{C}(t))=2n$. (This was proved by Nishioka for the single equation
$\mathrm{tr.deg}(\mathbb{C}(t)(y_1,y'_1,\ldots,y_n,y'_n)/\mathbb{C}(t))=2n$. (This was proved by Nishioka for the single equation 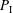 $P_{{\rm I}}$.) For generic Painlevé III and VI, we have a slightly weaker result:
$P_{{\rm I}}$.) For generic Painlevé III and VI, we have a slightly weaker result:  $\omega $-categoricity (in the sense of model theory) of the solution space, as described below. The results confirm old beliefs about the Painlevé transcendents.
$\omega $-categoricity (in the sense of model theory) of the solution space, as described below. The results confirm old beliefs about the Painlevé transcendents.