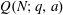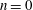Let $Q(N;q,a)$ be the number of squares in the arithmetic progression $qn+a$, for $n=0$,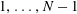$1,\ldots,N-1$, and let 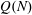$Q(N)$ be the maximum of 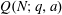$Q(N;q,a)$ over all non-trivial arithmetic progressions 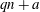$qn + a$. Rudin’s conjecture claims that 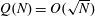$Q(N)=O(\sqrt{N})$, and in its stronger form that 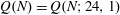$Q(N)=Q(N;24,1)$ if 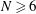$N\ge 6$. We prove the conjecture above for 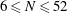$6\le N\le 52$. We even prove that the arithmetic progression $24n+1$ is the only one, up to equivalence, that contains $Q(N)$ squares for the values of 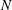$N$ such that 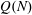$Q(N)$ increases, for 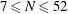$7\le N\le 52$ (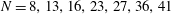$N=8,13,16,23,27,36,41$ and 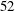$52$).

Supplementary materials are available with this article.

Let $k$ be a locally compact complete field with respect to a discrete valuation $v$. Let $ \mathcal{O} $ be the valuation ring, $\mathfrak{m}$ the maximal ideal and $F(x)\in \mathcal{O} [x] $ a monic separable polynomial of degree $n$. Let $\delta = v(\mathrm{Disc} (F))$. The Montes algorithm computes an OM factorization of $F$. The single-factor lifting algorithm derives from this data a factorization of $F(\mathrm{mod~} {\mathfrak{m}}^{\nu } )$, for a prescribed precision $\nu $. In this paper we find a new estimate for the complexity of the Montes algorithm, leading to an estimation of $O({n}^{2+ \epsilon } + {n}^{1+ \epsilon } {\delta }^{2+ \epsilon } + {n}^{2} {\nu }^{1+ \epsilon } )$ word operations for the complexity of the computation of a factorization of $F(\mathrm{mod~} {\mathfrak{m}}^{\nu } )$, assuming that the residue field of $k$ is small.

Let $C\subset C_1\times C_2$ be a curve of type $(d_1,d_2)$ in the product of the two curves $C_1$ and $C_2$. Let $\nu$ be a positive integer. We prove that if a certain inequality involving $d_1,\ d_2,\ \nu$, and the genera of the curves $C_1,\ C_2$, and $C$ is satisfied, then the set of points $\{P\in C(\bar{k})\mid[k(P):k]\leq \nu\}$ is finite for any number field $k$. We prove a similar result for integral points of bounded degree on $C$. These results are obtained as consequences of an inequality of Vojta which generalizes the Roth–Wirsing theorem to curves.