Let 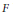 $F$ be a divisor on the blow-up
$F$ be a divisor on the blow-up 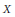 $X$ of
$X$ of 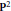 ${{\mathbf{P}}^{2}}$ at
${{\mathbf{P}}^{2}}$ at  $r$ general points
$r$ general points 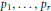 ${{p}_{1}},...,{{p}_{r}}$ and let
${{p}_{1}},...,{{p}_{r}}$ and let 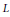 $L$ be the total transform of a line on
$L$ be the total transform of a line on 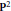 ${{\mathbf{P}}^{2}}$. An approach is presented for reducing the computation of the dimension of the cokernel of the natural map
${{\mathbf{P}}^{2}}$. An approach is presented for reducing the computation of the dimension of the cokernel of the natural map 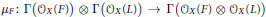 ${{\mu }_{F}}:\Gamma ({{\mathcal{O}}_{_{X}}}(F))\otimes \Gamma ({{\mathcal{O}}_{_{X}}}(L))\to \Gamma ({{\mathcal{O}}_{_{X}}}(F)\otimes {{\mathcal{O}}_{_{X}}}(L))$ to the case that
${{\mu }_{F}}:\Gamma ({{\mathcal{O}}_{_{X}}}(F))\otimes \Gamma ({{\mathcal{O}}_{_{X}}}(L))\to \Gamma ({{\mathcal{O}}_{_{X}}}(F)\otimes {{\mathcal{O}}_{_{X}}}(L))$ to the case that 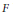 $F$ is ample. As an application, a formula for the dimension of the cokernel of
$F$ is ample. As an application, a formula for the dimension of the cokernel of 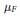 ${{\mu }_{_{F}}}$ is obtained when
${{\mu }_{_{F}}}$ is obtained when  $r\,=\,7$, completely solving the problem of determining the modules in minimal free resolutions of fat point subschemes
$r\,=\,7$, completely solving the problem of determining the modules in minimal free resolutions of fat point subschemes  ${{m}_{1}}\,{{p}_{1}}\,+\,\cdot \cdot \cdot \,+\,{{m}_{7}}\,{{p}_{7}}\,\subset \,{{\mathbf{P}}^{2}}$. All results hold for an arbitrary algebraically closed ground field
${{m}_{1}}\,{{p}_{1}}\,+\,\cdot \cdot \cdot \,+\,{{m}_{7}}\,{{p}_{7}}\,\subset \,{{\mathbf{P}}^{2}}$. All results hold for an arbitrary algebraically closed ground field 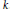 $k$.
$k$.
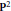 ${{\mathbf{P}}^{2}}$
${{\mathbf{P}}^{2}}$