Let $G$ be a semisimple Lie group with associated symmetric space $D$, and let $\unicode[STIX]{x1D6E4}\subset G$ be a cocompact arithmetic group. Let $\mathscr{L}$ be a lattice inside a $\mathbb{Z}\unicode[STIX]{x1D6E4}$-module arising from a rational finite-dimensional complex representation of $G$. Bergeron and Venkatesh recently gave a precise conjecture about the growth of the order of the torsion subgroup $H_{i}(\unicode[STIX]{x1D6E4}_{k};\mathscr{L})_{\operatorname{tors}}$ as $\unicode[STIX]{x1D6E4}_{k}$ ranges over a tower of congruence subgroups of $\unicode[STIX]{x1D6E4}$. In particular, they conjectured that the ratio $\log |H_{i}(\unicode[STIX]{x1D6E4}_{k};\mathscr{L})_{\operatorname{tors}}|/[\unicode[STIX]{x1D6E4}:\unicode[STIX]{x1D6E4}_{k}]$ should tend to a nonzero limit if and only if $i=(\dim (D)-1)/2$ and $G$ is a group of deficiency $1$. Furthermore, they gave a precise expression for the limit. In this paper, we investigate computationally the cohomology of several (non-cocompact) arithmetic groups, including $\operatorname{GL}_{n}(\mathbb{Z})$ for $n=3,4,5$ and $\operatorname{GL}_{2}(\mathscr{O})$ for various rings of integers, and observe its growth as a function of level. In all cases where our dataset is sufficiently large, we observe excellent agreement with the same limit as in the predictions of Bergeron–Venkatesh. Our data also prompts us to make two new conjectures on the growth of torsion not covered by the Bergeron–Venkatesh conjecture.

Van Wamelen [Math. Comp. 68 (1999) no. 225, 307–320] lists 19 curves of genus two over $\mathbf{Q}$ with complex multiplication (CM). However, for each curve, the CM-field turns out to be cyclic Galois over $\mathbf{Q}$, and the generic case of a non-Galois quartic CM-field did not feature in this list. The reason is that the field of definition in that case always contains the real quadratic subfield of the reflex field.

We extend Van Wamelen’s list to include curves of genus two defined over this real quadratic field. Our list therefore contains the smallest ‘generic’ examples of CM curves of genus two.

We explain our methods for obtaining this list, including a new height-reduction algorithm for arbitrary hyperelliptic curves over totally real number fields. Unlike Van Wamelen, we also give a proof of our list, which is made possible by our implementation of denominator bounds of Lauter and Viray for Igusa class polynomials.

We introduce a ‘limiting Frobenius structure’ attached to any degeneration of projective varieties over a finite field of characteristic p which satisfies a p-adic lifting assumption. Our limiting Frobenius structure is shown to be effectively computable in an appropriate sense for a degeneration of projective hypersurfaces. We conjecture that the limiting Frobenius structure relates to the rigid cohomology of a semistable limit of the degeneration through an analogue of the Clemens–Schmidt exact sequence. Our construction is illustrated, and conjecture supported, by a selection of explicit examples.

We state and verify up to weight 172 a conjecture on the existence of a certain generating set for spaces of classical Siegel modular forms. This conjecture is particularly useful for calculations involving Fourier expansions. Using this generating set, we verify the Böcherer conjecture for nonrational eigenforms and discriminants with class number greater than one. As a further application we verify another conjecture for weights up to 150 and investigate an analog of the Victor–Miller basis. Additionally, we describe some arithmetic properties of the basis we found.

Constants with formulae of the form treated by D. Bailey, P. Borwein, and S. Plouffe ($b$ formulae to a given base $b$) have interesting computational properties, such as allowing single digits in their base $b$ expansion to be independently computed, and there are hints that they should be normal numbers, i.e., that their base $b$ digits are randomly distributed. We study a formally limited subset of BBP formulae, which we call Machin-type BBP formulae, for which it is relatively easy to determine whether or not a given constant $K$ has a Machin-type BBP formula. In particular, given $b\,\in \,\mathbb{N},\,b\,>\,2,\,b$ not a proper power, a $b$-ary Machin-type BBP arctangent formula for $K$ is a formula of the form $k\,=\,{{\Sigma }_{m}}\,{{a}_{m}}\,\arctan \,(-{{b}^{-m}}),\,{{a}_{m}}\,\in \,\mathbb{Q}$ , while when 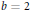$b\,=\,2$, we also allow terms of the form 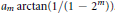${{a}_{m}}\,\arctan \,(1/1\,-\,{{2}^{m}}))$ . Of particular interest, we show that $\pi$ has no Machin-type BBP arctangent formula when 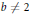$b\,\ne \,2$. To the best of our knowledge, when there is no Machin-type BBP formula for a constant then no BBP formula of any form is known for that constant.

We present a new approach to the problem of computing the zeta function of a hypersurface over a finite field. For a hypersurface defined by a polynomial of degree $d$ in $n$ variables over the field of $q$ elements, one desires an algorithm whose running time is a polynomial function of $d^n \log(q)$. (Here we assume $d \geq 2$, for otherwise the problem is easy.) The case $n = 1$ is related to univariate polynomial factorisation and is comparatively straightforward. When $n = 2$ one is counting points on curves, and the method of Schoof and Pila yields a complexity of $\log(q)^{C_d}$, where the function $C_d$ depends exponentially on $d$. For arbitrary $n$, the theorem of the author and Wan gives a complexity which is a polynomial function of $(pd^n \log(q))^n$, where $p$ is the characteristic of the field. A complexity estimate of this form can also be achieved for smooth hypersurfaces using the method of Kedlaya, although this has only been worked out in full for curves. The new approach we present should yield a complexity which is a small polynomial function of $pd^n\log(q)$. In this paper, we work this out in full for Artin–Schreier hypersurfaces defined by equations of the form $Z^p - Z = f$, where the polynomial $f$ has a diagonal leading form. The method utilises a relative $p$-adic cohomology theory for families of hypersurfaces, due in essence to Dwork. As a corollary of our main theorem, we obtain the following curious result. Let $f$ be a multivariate polynomial with integer coefficients whose leading form is diagonal. There exists an explicit deterministic algorithm which takes as input a prime $p$, outputs the number of solutions to the congruence equation $f = 0 \bmod{p}$, and runs in ${\mathcal O}(p^{2 + \varepsilon})$ bit operations, for any $\varepsilon > 0$. This improves upon the elementary estimate of ${\mathcal O}(p^{n-1 + \varepsilon})$ bit operations, where $n$ is the number of variables, which can be achieved using Berlekamp's root counting algorithm.

Recently there has been tremendous interest in counting the number of integral points in $n$-dimensional tetrahedra with non-integral vertices due to its applications in primality testing and factoring in number theory and in singularities theory. The purpose of this note is to formulate a conjecture on sharp upper estimate of the number of integral points in $n$-dimensional tetrahedra with non-integral vertices. We show that this conjecture is true for low dimensional cases as well as in the case of homogeneous $n$-dimensional tetrahedra. We also show that the Bernoulli polynomials play a role in this counting.

If $f({{x}_{1}},...,{{x}_{k}})$ is a polynomial with complex coefficients, the Mahler measure of $f$ , $M(f)$ is defined to be the geometric mean of $|f|$ over the $k$-torus ${{\mathbb{T}}^{k}}$. We construct a sequence of approximations ${{M}_{n}}\,(f)$ which satisfy $-d{{2}^{-n}}\,\log \,2\,+\,\log \,{{M}_{n}}(f)\,\le \,\log \,M(f)\,\le \,\log \,{{M}_{n}}(f)$. We use these to prove that $M(f)$ is a continuous function of the coefficients of $f$ for polynomials of fixed total degree $d$. Since ${{M}_{n}}\,(f)$ can be computed in a finite number of arithmetic operations from the coefficients of $f$ this also demonstrates an effective (but impractical) method for computing $M(f)$ to arbitrary accuracy.