We construct a new family of quintic non-Pólya fields with large Pólya groups. We show that the Pólya number of such a field never exceeds five times the size of its Pólya group. Finally, we show that these non-Pólya fields are nonmonogenic of field index one.

An explicit formula forthe mean value of 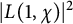$\vert L(1,\chi )\vert ^2$ is known, where 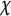$\chi $ runs over all odd primitive Dirichlet characters of prime conductors p. Bounds on the relative class number of the cyclotomic field 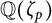${\mathbb Q}(\zeta _p)$ follow. Lately, the authors obtained that the mean value of 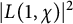$\vert L(1,\chi )\vert ^2$ is asymptotic to $\pi ^2/6$, where 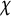$\chi $ runs over all odd primitive Dirichlet characters of prime conductors $p\equiv 1\ \ \pmod {2d}$ which are trivial on a subgroup H of odd order d of the multiplicative group $({\mathbb Z}/p{\mathbb Z})^*$, provided that 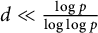$d\ll \frac {\log p}{\log \log p}$. Bounds on the relative class number of the subfield of degree 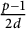$\frac {p-1}{2d}$ of the cyclotomic field 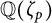${\mathbb Q}(\zeta _p)$ follow. Here, for a given integer 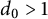$d_0>1$, we consider the same questions for the nonprimitive odd Dirichlet characters 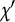$\chi '$ modulo $d_0p$ induced by the odd primitive characters 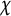$\chi $ modulo p. We obtain new estimates for Dedekind sums and deduce that the mean value of 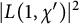$\vert L(1,\chi ')\vert ^2$ is asymptotic to 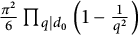$\frac {\pi ^2}{6}\prod _{q\mid d_0}\left (1-\frac {1}{q^2}\right )$, where $\chi $ runs over all odd primitive Dirichlet characters of prime conductors p which are trivial on a subgroup H of odd order 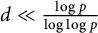$d\ll \frac {\log p}{\log \log p}$. As a consequence, we improve the previous bounds on the relative class number of the subfield of degree 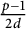$\frac {p-1}{2d}$ of the cyclotomic field 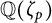${\mathbb Q}(\zeta _p)$. Moreover, we give a method to obtain explicit formulas and use Mersenne primes to show that our restriction on d is essentially sharp.

Let $m>1$ and $\mathfrak {d} \neq 0$ be integers such that $v_{p}(\mathfrak {d}) \neq m$ for any prime p. We construct a matrix $A(\mathfrak {d})$ of size $(m-1) \times (m-1)$ depending on only of $\mathfrak {d}$ with the following property: For any tame $ \mathbb {Z}/m \mathbb {Z}$ -number field K of discriminant $\mathfrak {d}$ , the matrix $A(\mathfrak {d})$ represents the Gram matrix of the integral trace-zero form of K. In particular, we have that the integral trace-zero form of tame cyclic number fields is determined by the degree and discriminant of the field. Furthermore, if in addition to the above hypotheses, we consider real number fields, then the shape is also determined by the degree and the discriminant.

The aim of this paper is to study circular units in the compositum K of t cyclic extensions of ${\mathbb {Q}}$ ( $t\ge 2$ ) of the same odd prime degree $\ell $ . If these fields are pairwise arithmetically orthogonal and the number s of primes ramifying in $K/{\mathbb {Q}}$ is larger than $t,$ then a nontrivial root $\varepsilon $ of the top generator $\eta $ of the group of circular units of K is constructed. This explicit unit $\varepsilon $ is used to define an enlarged group of circular units of K, to show that $\ell ^{(s-t)\ell ^{t-1}}$ divides the class number of K, and to prove an annihilation statement for the ideal class group of K.

We give an algebraic proof of a class number formula for dihedral extensions of number fields of degree 2q, where q is any odd integer. Our formula expresses the ratio of class numbers as a ratio of orders of cohomology groups of units and allows one to recover similar formulas which have appeared in the literature. As a corollary of our main result, we obtain explicit bounds on the (finitely many) possible values which can occur as ratio of class numbers in dihedral extensions. Such bounds are obtained by arithmetic means, without resorting to deep integral representation theory.

The aim of this paper is to study the group of elliptic units of a cyclic extension $L$ of an imaginary quadratic field $K$ such that the degree $[L:K]$ is a power of an odd prime $p$. We construct an explicit root of the usual top generator of this group, and we use it to obtain an annihilation result of the $p$-Sylow subgroup of the ideal class group of $L$.

In this paper we study the number of rational points on curves in an ensemble of abelian covers of the projective line: let $\ell$ be a prime, $q$ a prime power and consider the ensemble ${\mathcal{H}}_{g,\ell }$ of $\ell$-cyclic covers of $\mathbb{P}_{\mathbb{F}_{q}}^{1}$ of genus $g$. We assume that $q\not \equiv 0,1~\text{mod}~\ell$. If $2g+2\ell -2\not \equiv 0~\text{mod}~(\ell -1)\operatorname{ord}_{\ell }(q)$, then ${\mathcal{H}}_{g,\ell }$ is empty. Otherwise, the number of rational points on a random curve in ${\mathcal{H}}_{g,\ell }$ distributes as $\sum _{i=1}^{q+1}X_{i}$ as $g\rightarrow \infty$, where $X_{1},\ldots ,X_{q+1}$ are independent and identically distributed random variables taking the values $0$ and $\ell$ with probabilities $(\ell -1)/\ell$ and $1/\ell$, respectively. The novelty of our result is that it works in the absence of a primitive $\ell$th root of unity, the presence of which was crucial in previous studies.

Let $N/ F$ be an odd-degree Galois extension of number fields with Galois group $G$ and rings of integers ${\mathfrak{O}}_{N} $ and ${\mathfrak{O}}_{F} = \mathfrak{O}$. Let $ \mathcal{A} $ be the unique fractional ${\mathfrak{O}}_{N} $-ideal with square equal to the inverse different of $N/ F$. B. Erez showed that $ \mathcal{A} $ is a locally free $\mathfrak{O}[G] $-module if and only if $N/ F$ is a so-called weakly ramified extension. Although a number of results have been proved regarding the freeness of $ \mathcal{A} $ as a $ \mathbb{Z} [G] $-module, the question remains open. In this paper we prove that $ \mathcal{A} $ is free as a $ \mathbb{Z} [G] $-module provided that $N/ F$ is weakly ramified and under the hypothesis that for every prime $\wp $ of $\mathfrak{O}$ which ramifies wildly in $N/ F$, the decomposition group is abelian, the ramification group is cyclic and $\wp $ is unramified in $F/ \mathbb{Q} $. We make crucial use of a construction due to the first author which uses Dwork’s exponential power series to describe self-dual integral normal bases in Lubin–Tate extensions of local fields. This yields a new and striking relationship between the local norm-resolvent and the Galois Gauss sum involved. Our results generalise work of the second author concerning the case of base field $ \mathbb{Q} $.

For a number field K and a finite abelian group G, we determine the probabilities of various local completions of a random G-extension of K when extensions are ordered by conductor. In particular, for a fixed prime ℘ of K, we determine the probability that ℘ splits into r primes in a random G-extension of K that is unramified at ℘. We find that these probabilities are nicely behaved and mostly independent. This is in analogy to Chebotarev’s density theorem, which gives the probability that in a fixed extension a random prime of K splits into r primes in the extension. We also give the asymptotics for the number of G-extensions with bounded conductor. In fact, we give a class of extension invariants, including conductor, for which we obtain the same counting and probabilistic results. In contrast, we prove that neither the analogy with the Chebotarev probabilities nor the independence of probabilities holds when extensions are ordered by discriminant.

We compute the minimal polynomials of the Ramanujan values ${{t}_{n}}$, where $n\,\equiv \,11\,\bmod \,24$, using the Shimura reciprocity law. These polynomials can be used for defining the Hilbert class field of the imaginary quadratic field $\mathbb{Q}\left( \sqrt{-n} \right)$ and have much smaller coefficients than the Hilbert polynomials.

We obtain Hauptmoduls of genus zero congruence subgroups of the type $\Gamma _{0}^{+}\left( p \right)\,\,:={{\Gamma }_{0}}\left( p \right)+{{w}_{p}}$, where $p$ is a prime and ${{w}_{p}}$ is the Atkin–Lehner involution. We then use the Hauptmoduls, along with modular functions on ${{\Gamma }_{1}}\left( p \right)$ to construct families of cyclic extensions of quadratic number fields. Further examples of cyclic extension of bi-quadratic and tri-quadratic number fields are also given.

We prove, for a field $K$ which is cyclic of odd prime power degree over the rationals, that the annihilator of the quotient of the units of $K$ by a suitable large subgroup (constructed from circular units) annihilates what we call the non-genus part of the class group. This leads to stronger annihilation results for the whole class group than a routine application of the Rubin–Thaine method would produce, since the part of the class group determined by genus theory has an obvious large annihilator which is not detected by that method; this is our reason for concentrating on the non-genus part. The present work builds on and strengthens previous work of the authors; the proofs are more conceptual now, and we are also able to construct an example which demonstrates that our results cannot be easily sharpened further.

For an abelian totally real number field F and an odd prime number p which splits totally in F, we present a functorial approach to special “p-units” previously built by D. Solomon using “wild” Euler systems. This allows us to prove a conjecture of Solomon on the annihilation of the p-class group of F (in the particular context here), as well as related annihilation results and index formulae.

There is in the literature a lot of determinant formulae involving the relative class number of an imaginary abelian field. Usually such a formula contains a factor which is equal to zero for many fields and so it gives no information about the class number of these fields. The aim of this paper is to show a way of obtaining most of these formulae in a unique fashion, namely by means of the Stickelberger ideal. Moreover some new and non-vanishing formulae are derived by a modification of Ramachandra’s construction of independent cyclotomic units.

A new infinite product ${{t}_{n}}$ was introduced by S. Ramanujan on the last page of his third notebook. In this paper, we prove Ramanujan’s assertions about ${{t}_{n}}$ by establishing new connections between the modular $j$-invariant and Ramanujan’s cubic theory of elliptic functions to alternative bases. We also show that for certain integers $n$, ${{t}_{n}}$ generates the Hilbert class field of $\mathbb{Q}\left( \sqrt{-n} \right)$. This shows that ${{t}_{n}}$ is a new class invariant according to H. Weber’s definition of class invariants.

A formula is obtained for the rank of the 2-Sylow subgroup of the ideal class group of imaginary bicyclic biquadratic fields. This formula involves the number of primes that ramify in the field, the ranks of the 2-Sylow subgroups of the ideal class groups of the quadratic subfields and the rank of a Z2-matrix determined by Legendre symbols involving pairs of ramified primes. As applications, all subfields with both 2- class and class group Z2×Z2 are determined. The final results assume the completeness of D. A. Buell’s list of imaginary fields with small class numbers.

Some formulas for multiplicities of pure cubic discriminants are generalized to the case of a pure field of arbitrary odd prime degree.