We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this article we investigate the average order of the arithmetical function
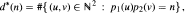
where p1(t), p2(t) are polynomials in Z [t], of equal degree, positive and increasing for t ≥ 1. Using the modern method for the estimation of exponential sums ("Discrete Hardy-Littlewood Method"), we establish an asymptotic result which is as sharp as the best one known for the classical divisor problem.
Let {x} denote the fractional part of x. We find an asymptotic formula of , where k is any positive integer and a is any real number ≥ 1, and so for the sum ∑n<xf(n), where f(n) belongs to a class of additive functions.
Let d(n;l,k) denote the number of divisors of the positive integer n which are congruent to I modulo k. The objective of the present paper is to prove that (for some exponent θ<⅓)
holds uniformly in l, k and x satisfying 1≤l≤k≤x. This improves a recent result due to R. A. Smith and M. V. Subbarao [3].
Let
It is proved that the function f reaches its maximum for n = 6 983 776 800, and that maxn≥2f(n) = 1.5379. The proof deals with superior highly composite numbers introduced by Ramanujan.
