In this paper, the boundedness from below of multiplication operators between  $\alpha$-Bloch spaces
$\alpha$-Bloch spaces 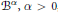 ${{B}^{\alpha }},\,\alpha \,>\,0$, on the unit disk
${{B}^{\alpha }},\,\alpha \,>\,0$, on the unit disk 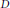 $D$ is studied completely. For a bounded multiplication operator
$D$ is studied completely. For a bounded multiplication operator 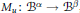 ${{M}_{u}}\,:\,{{B}^{\alpha }}\,\to \,{{B}^{\beta }}$, defined by
${{M}_{u}}\,:\,{{B}^{\alpha }}\,\to \,{{B}^{\beta }}$, defined by 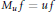 ${{M}_{u}}f\,=\,uf$ for
${{M}_{u}}f\,=\,uf$ for 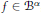 $f\,\in \,{{B}^{\alpha }}$, we prove the following result:
$f\,\in \,{{B}^{\alpha }}$, we prove the following result:
(i) If  $0<\beta <\alpha ,\,\text{or}\,\text{0}<\alpha \le \text{1}\,\text{and}\,\alpha <\beta \text{,}\,{{M}_{u}}$ is not bounded below;
$0<\beta <\alpha ,\,\text{or}\,\text{0}<\alpha \le \text{1}\,\text{and}\,\alpha <\beta \text{,}\,{{M}_{u}}$ is not bounded below;
(ii) if 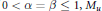 $0\,<\,\alpha \,=\,\beta \,\le \,1,\,{{M}_{u}}$ is bounded below if and only if lim
$0\,<\,\alpha \,=\,\beta \,\le \,1,\,{{M}_{u}}$ is bounded below if and only if lim 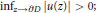 ${{\inf }_{z\to \partial D}}\,\left| u\left( z \right) \right|\,>\,0;$
${{\inf }_{z\to \partial D}}\,\left| u\left( z \right) \right|\,>\,0;$
(iii) if 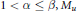 $1\,<\,\alpha \,\le \,\beta ,\,{{M}_{u}}$ is bounded below if and only if there exist a
$1\,<\,\alpha \,\le \,\beta ,\,{{M}_{u}}$ is bounded below if and only if there exist a 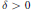 $\delta \,>\,0$ and a positive
$\delta \,>\,0$ and a positive 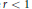 $r\,<\,1$ such that for every point
$r\,<\,1$ such that for every point 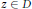 $z\,\in \,D$ there is a point
$z\,\in \,D$ there is a point 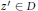 ${{z}^{'}}\,\in \,D$ with the property
${{z}^{'}}\,\in \,D$ with the property 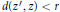 $d\left( {{z}^{'}},\,z \right)\,<\,r$ and
$d\left( {{z}^{'}},\,z \right)\,<\,r$ and 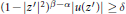 ${{\left( 1\,-\,{{\left| {{z}^{'}} \right|}^{2}} \right)}^{\beta -\alpha }}\left| u\left( {{z}^{'}} \right) \right|\,\ge \,\delta$, where
${{\left( 1\,-\,{{\left| {{z}^{'}} \right|}^{2}} \right)}^{\beta -\alpha }}\left| u\left( {{z}^{'}} \right) \right|\,\ge \,\delta$, where 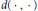 $d\left( \cdot ,\,\cdot \right)$ denotes the pseudo-distance on
$d\left( \cdot ,\,\cdot \right)$ denotes the pseudo-distance on  $D$.
$D$.