We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let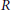 
$R$ be an arbitrary ring and let 
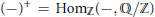${{\left( - \right)}^{+}}\,=\,\text{Ho}{{\text{m}}_{\mathbb{Z}}}\left( -,\,{\mathbb{Q}}/{\mathbb{Z}}\; \right)$, where 
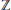$\mathbb{Z}$ is the ring of integers and 
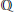$\mathbb{Q}$ is the ring of rational numbers. Let 
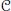$\mathcal{C}$ be a subcategory of left 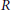$R$-modules and 
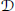$\mathcal{D}$ a subcategory of right 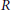$R$-modules such that 
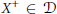${{X}^{+}}\,\in \,\mathcal{D}$ for any 
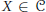$X\,\in \,\mathcal{C}$ and all modules in 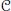$\mathcal{C}$ are pure injective. Then a homomorphism 
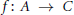$f:\,A\to \,C$ of left 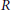$R$-modules with 
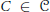$C\,\in \,\mathcal{C}$ is a 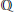$\mathcal{C}$-(pre)envelope of 
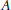$A$ provided 
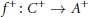${{f}^{+}}:\,{{C}^{+}}\,\to \,{{A}^{+}}$ is a 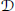$\mathcal{D}$-(pre)cover of 
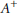${{A}^{+}}$. Some applications of this result are given.
We show that if the given cotorsion pair 
in the category of modules is complete and hereditary, then both of the induced cotorsion pairs in the category of complexes are complete. We also give a cofibrantly generated model structure that can be regarded as a generalization of the projective model structure.
